SPIN & Promela
Page Contents
References
- The SPIN Model Checker: Primer And Reference Manual, G. Holzmann.
- Temporal Logics I: Theory, Daniel Shahaf, Tel-Aviv University, November 2007
- Lecture 25, Linear Temporal Logic, Models of Software Systems, Fall 1999, Carnegie Mellon University
- https://www.cs.utexas.edu/~mooney/cs343/slide-handouts/fopc.4.pdf
- http://www.cs.tau.ac.il/~annaz/teaching/TAU_winter08/Seminar/daniel.pdf
- http://www.cis.upenn.edu/~fisman/documents/EF_HBMC14.pdf
To Read
https://www.research.ibm.com/haifa/conferences/hvc2010/present/Testing_and_Debugging_Concurrent_Software.pdf
Promela Notes
Symbolic Names & Variables
Almost equivalent of a C enum. Use the mtype declaration to
introduce symbolic names for constant values.
mtype = {SYM_NAME 1, SYM_NAME_2, ... };
mtype my_variable = SUM_NAME_1 // Default would be zero
The symbol names have unique positive integer Ids.
The word mtype is short for "message type" and although
usually defining values for types of messages between promela-processes can be used
otherwise.
In later versions of spin, subtypes of the form mtype:<sub-type-name> = { ... }
can also be used.
Promela Processes
The keyword proctype declares a promela-process. May be preceeded with the keyword
active to start an instance of the promela-process automatically.
Note use of "promela-process" v.s. "process".
Example:
active [n] proctype some_name()
{
printf("Do something\n")
}
The above starts n promela-processes of type some_name. The
[n] can be ommitted, and is so it is like writing [1].
When more than 1 promela-process could continue to run, the choice of which gets to run is randomly made. This means no assumptions are made about scheduling.
Processes can be run manually from the init block, although this is less
favourable as it creates another process (the init process), which could bloat
a verification state space unecessarily.
proctype some_name(int a)
{
printf("Do something %d\n", a)
}
init {
run some_name(1);
run some_name(2);
}
We can constrain a process using the provided keyword. A promela-process
cannot take any step unless the provided class is true.
active [n] proctype some_name() provided (some-boolean-expression)
{
printf("Do something\n"); // This line won't execute until `some-boolean-expression` is true
printf("Do something else\n") // Neither will this line.
// Its like each line is guarded by `some-boolean-expression`
}
Scope
The only scopes are global and process-local. Thus variables cannot be
scoped to, for example, an if statement. Variables cannot be used until they
are declared - there is no JavaScript style hoisting.
In the global scope all promela-processes can see the variable. In the process-local scope only the process can see the variable.
Data Types
| bit | 0, 1 |
| bool | false, true |
| byte | 0...255 |
| chan | 1...255 |
| mtype | 1...255 |
| pid | 0...255 |
| short | -215...215-1 |
| int | -231...231-1 |
| unsigned | 0...2n-1 |
Data Structures
Thing C-style structures
typedef MyType {
short myShort = 3;
byte myByte;
unsigned myUnsigned : 5 /*< 5 bit unsigned integer */
};
proctype myProc(MyType t) {
t.myShort = 3;
}
Flow Control & Execution
Execution
All conditional statements guard execution, and can block, whether or not they have any instructions to execute after the guard or not.
... (x == y) -> ...
In the above snippet the promela-process executing the code will block at the line
(x == y) -> until the condition is true. As there are no statements after the
arrow, it will just block and when the condition becomes true continue onto the next line.
In promela every type of statement can act as a guard in any context, even when used
standalone. But note, it should not have side effects! Only run(...)
is allowed to have a side effect.
Things like prints or assignments are immediately executable.
Expressions which evaluate to false guaranteeably have no side effects.
Do Loop
A do loop looks like the following. It consists of a set of guard conditions.
The guard conditions are evaluated on each iteration.
If a guard evaluates to true then it is said to be executable.
If no guard is executable the promela-process blocks until one is. Otherwise one branch out of the set of all executable branches is chosen at random.
do
:: boolean-guard-1 -> printf("Execute choice 1"); // What follows the guard is the
printf("do something 1") // "execution sequence "
:: boolean-guard-2 -> printf("Execute choice 2");
printf("do something 2") // Note last statement in sequence
// has no trailing semi-colon. The semi-
// colon is a seperator, not a terminator.
...
:: boolean-guard-n -> printf("Execute choice n");
printf("do something n")
od
Exit a loop using the break statement or the goto statement.
The arrow is just a nice syntactic sugar for the guard. It is equivalent to a semi-colon. We could write it like this:
do
:: boolean-guard-1; printf("Execute choice 1");
printf("do something 1")
:: boolean-guard-2; printf("Execute choice 2");
printf("do something 2")
...
od
To avoid blocking if no guard is true you can use the else keyword:
do
:: boolean-guard-1 -> printf("Execute choice 1")
:: else -> printf("Won't block and does busy waiting")
od
The keyword else will only evaluate to true if and only if
all other guards are false. When else is selected it is therefore the
only executable option.
Selection / If
Same execuation rules as for do loop:
if
:: boolean-guard-1; printf("Execute choice 1");
printf("do something 1")
:: boolean-guard-2; printf("Execute choice 2");
printf("do something 2")
...
fi
Atomic Sequences
All statements in an atomic sequence are executed without interruption by another promela-process. It is a type of compund statement.
An atomic sequence can have a guard (the first statement), in which case the guard determines whether the sequence runs, and when it does run, it does so atomically.
Write a sequence as follows:
atomic { boolean-guard-condition -> statment1; statement2; ... }
Sequences can included flow control and be non-deterministic (control structures with multiple true guards can randomly choose a path).
Warning: If any statement in the sequence, other than the guard blocks, the atomicity is broken at the point of blocking and re-gained when unblocking occurs.
Deterministic Steps
Like atomic sequences except no non-determinism (control structures will deterministically choose a path when multiple guards are true), no jumps, and may not contain blocking statements other than the guard. It is a type of compund statement.
Macros / Inline Functions
An inline "function" behaves, in many ways, like a C pre-processor macro does.
The word "function" is in quotes because it is not a function! It is just some
nice syntactic sugar that defines a macro.
inline macro_name(param1, ...) {
// Do some stuff
}
To see the result of preprocessing pass the -I option to SPIN.
Not that because this is a pre-processor substition the statements in the inline body are not atomic unless you explicitly mark them so.
Special Variables
_pid
Read-only, local variable. Evaluates to numeric ID of currently running promela-process.
Variables holding numeric IDs should be of type pid. E.g.:
pid myvar = _pid;
timeout
Read-only boolean variable. Is true when no other statement in the entire system is executable. False otherwise.
Don't Care Dummy Write Variable
The underscore (_).
Message Passing
Promela channels are used to pass messages between asynchronous promela-processes. Every channel has its own unique ID.
Declaring Channels
Declare channels using the chan keyword:
mtype = { some, set, of, symbolic_constants };
...
chan CHAN_NAME = [n] of { mtype, ... }
Where n is zero or a positive integer declaring how many items the channel
can hold until it blocks. Thus if n == 0, the channel will immediately block
a sender until a receiver reads the value being sent (creates a rendez-vous). If
n == 1 the sender can send 1 value to an empty channel without blocking. If the
channel already has a message in it the sender would block, and so on...
The type of message is either a symbolic constant, in which case, for example we could declare:
chan CHAN_NAME = [1] of {mtype}
Or the message can be an aggregate (think structure in C):
chan CHAN_NAME = [1] of {mtype, int, bit, user-defined, ...}
Sending / Receiving From Channels
To send a message into a channel:
CHAN_NAME!expr1[, expr2, ...] CHAN_NAME!expr1(expr2[, ...]) // equivalent to the above
The default is that the send is executable only if there is space in the channel otherwise it will block.
To receive a message of particular type from a channel:
CHAN_NAME?var1[, var2, ...] CHAN_NAME?var1(var2[, ...]) // equivalent to the above
The default is that the receive is executable only if there is a message in the channel otherwise it will block.
The above will receive messages into the listed variables. If you specify constants instead, the statement is only executable if the constants match the message to be read.
If we want to use a variable as-if it were a constant to constrain what can be received
surround the variable with eval(varname).
Constrain Channel Usage (Make Verification Quicker)
Use xr, meaning exclusive read, and xs for exculsive
send as shown:
chan b = [1] of { ... }
chan c = [1] of { ... }
active proctype proc1() {
xs b; /* assert proc1 only sends to b */
xr c; /* assert proc2 only receives from c */
}
Helps reduce amount of work verification algorithm has to do by providing some hints about the channel usage in the model. They are assertions that will be checked during a validation.
Other Channel Operations
Length: Use len(chanName) to get the number of messages in a channel.
Emptiness: Use empty/nempty(chanName) to see if channel is empty/not-empty.
Full: Use full/nfull(chanName) to see if channel is full/not-full.
Would progress: To find out if a send/receive would be executable you cannot use chan!expr or
chan?const_or_var as these expressions both have side effects.
Instead use chan![expr] or chan?[const_or_var]. These only
examine the precondition for the execution of the statement, but don't actually execute it.
Read but don't dequeue: chanName?<var_or_const>
Review Of Propositional Logic
A quick recap of propositional logic [Ref].
A proposition is a statement or sentence that is either True or False. For example, "it is raining" is a proposition. It can only ever be True or False and has a precise and unambiguous meaning.
Propositions are usually represented using propositional variables. Popositional logic deals with how individual propositions can be combined to produce more complex logical popositions. For example, let mean "it is raining" and "b" mean "it is flooding". We can then construct logical statements like to mean "it is raining and flooding" or meaing "if it is flooding then it is raining".
Review Of Predicate Logic
Lets do a very quick recap of some First Order Predicate Logic (FOPL) stuff [Ref].
A predicate represents a property of, or a relation between terms that is either true or false. For example, or , for example.
Standard logical operators can connect predicates .
Predicates "extend" or add a greater flexibility to propositional logic. In propositial logic, we would have to define 2 propositions = "James is alive" and = "John is alive". But in predicate logic we just define the predicate and apply it to our objects of interest, i.e., and . Because of this extra power, predicate logic can be used to reason about sets of objects. We don't need to define a proposition for each member of a set; now we define a predicate applied over a set in a more abstract way using quantifiers.
Quantifiers allow entire ranges of objects to be reasoned about. For example. . The universal quantifier says that something is true for all values of a variable - asserts that the predicate must be true for every value in a set. The existential quantifier says that a predicate must be true for at least one value.
The "scope" of a quantifier is everything that occurs after it (inside any brackets it belongs to). So is equivalent to So , i.e., everything in the entire universe is purple and a lemon. But in this - - the two variables are independent of eachother, although logically they express the same thing.
When quantifiers nest their "scopes" do too. So something like means that every child has a parent. It was eqivalent to writing . Note that when the nested quanitifers are not the same that the order matters: means that there exists a child for whom everyone is their parent!
Scope can also be used with variables of the same name where the inner hides the outer: . The in pred1 is existentially quantified and the in pred2 is universally quantified.
The quantifiers are related as follows:
Linear Temporal Logic (LTL)
First order predicate logic (FOPL, aka just "predicate logic") can reason about a system state at one moment in time. Using it one can talk about things like "James is alive". In the current moment this is true. But what about tomorrow, or indeed eventually? We all die sometime. We cannot express this using FOPL. This is where LTL comes in.
LTL is used to reason about the change in system states over time. We care about:
- Saftey: Nothing "bad"will happen. (Never conditions).
- Liveness: Something "good" will happen.
- Fairness: Processes can make progress - no starvation.
To talk about LTL, we need to do a quick review of automata...
Automata
Finite State Automaton is defined by a tuple where:
is the initiatial state such that
is a finite set of labels
is a set of transitions, , and
is a set of final states
For example, look at the following automaton:
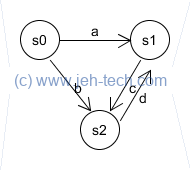
For this automaton we have:
is the initiatial state such that
, and
Runs Through Finite Automatons
A run of a FA is a an ordered sequence of transitions - possibly infinite. For example, if is the run, and is the set of all possible transitions within the autonaton, then . A concrete, finite, example using the automaton above could be .
An accepting run is one where the final state is in the set of end states (implicity all the end states are seen as accepting). This applies to the concrete example just given. Runs defined in this way are all terminating.
But what about infinite loops through states? The same automaton we saw above provides the possibility for infinite runs that oscillate between and . For example: .
These may or may not be a good thing. These runs must be infinite and are referred to as -runs. The set of transitions that occur infinitely often in the run are denoted and other states .
- : transitions occuring infinitely often.
- : transitions that occur a finite number of times.
An accepting -run is one where - the Buchi acceptance definition. I.e., an accepting -run is a loop when at least one state is visited infinitely often.
This rule is extended to finite runs using the stutter extension rule which adds an end state that can be repeated infinitely often.
Call an instance of an -run. If the states in the run are , then:
- - this is called the suffix from position . The indexing starts at 1, so and so on.
Into The LTL
LTL extends classical logic by adding new operators:
- : "Always": Holds is is true henceforth (in the next position ) until the end of time.
- : "Eventually": Holds if holds someday, that is unspecified from today onwards,.
- : "Next time": Holds if holds at the next moment in time, .
- : "Until": Holds if does not become false before becomes true.
Two variants:- Strong until.
- Weak until.
When a formula holds for an -run , we write .
Weak Until
The weak until operator is expressed by the following: Which, if you're anything like me, makes you want to curl up in the corner of the room and cry!
So, can we break this down any? Well, Remember, means the states . So this chunk of the formula means "p until q holds for all the states in suffix from position .
"" means "if an only if". Then, Means that holds (i.e., is true) in the state of the -run, .
So far it is saying that the statement "p is true until q is true (p until q)" is true for the run-suffix, starting at state , if and only if is true at state in the run or...
Lets have a look at that "or..." bit next.
We can deal with the next bit in one chunk: This is saying that is true in state of the run and p-until-q holds for the suffix of the run starting at state .
So, in total we have, "p is true until q is true (p until q)" is true for the run-suffix, starting at state , if and only if is true at state in the run, or is true at state and "p is true until q is true (p until q)" holds for the next suffix startin at state .
This is a recursive definition! Starting at the first state in our run, either is true or is true recurse... therefore, we never actually know or require that ever become true - we keep putting it off!
Strong Until
Unlike week until, where for , was not required to ever become true (as we could keep putting it off), strong-until does require that come true. It is defined as follows:
Always
Always means that something holds invariantly true throughout a run. So, always means until ... hmmm. Lets break it down. If we consider weak until, we know that does not require to ever become true and would therefore always be true if were to hold. Thats why it is defined this way.
Eventually
A property will eventually become true at least once in a run.
Next
Combinations Of LTL Operators
Recurrence is expressed as , i.e., "always eventually becomes true". This expresses an invariance.
Stability is expressed as ,i.e., "eventally always ". This expresses a guarantee.
A response is shown as . This works because if occurs, for the expression to be true that must eventually become true.
A precidence (a usage, tradition, or standard to be followed in the future) is expressed as . I.e., implies that will be true until becomes true. The property is the precedent that holds until a new precedent is set.
A correlation is decribed as .
Other commonly used rules include:
Going From Non-Temporal To Temporal Logic
The SPIN book uses the example of . In the context of LTL, what does this mean without any temporal operators? A "true" LTL statement implies means that this must hold for every run of the system: . Without temporal operators this just applies for the first state in the run. States beyond that... it says nothing about!
To "implement" this implication in LTL, a more accurate description could be . In other words, is eventuall true and it is always the case that becoming true means that will eventually become true sometime strictly after.
SPIN Notes
Types Of Claims
SPIN is concerned about what is and isn't possible, not what is good or bad, or probable and improbable.
To allow SPIN to tell you about what is and isn't possible you need to make claims about your model. You can make,
- Claims about reachable/unreachable states, and
- Claims about feasible/infeasible executions (i.e., paths forming state transitions). E.g., every time state P is visited, subsequently state Q should eventually be visited.
SPIN automatically checks for deadlocks (unintended end states).
A system invariant should be true for every reachable state in the system. A process invariant is true only for every state reachable in a process.
Basic Assertions
Basic assertions use the assert(expr) statement. The expr should
always evaluate to true (or non-zero int). If it does not SPIN
considers this an error and fails the model.
End States
Only default valid end state is when every promela-process has terminated. Verification checks no invalid end states can be reached, which is a saftey issue.
To mark alternative states as valid end states use end-state labels. Labels must
be unique to their proctype. Every label that starts with the prefix end
marks a valid end state.
To make sure all promela-processes are in a valid end state at the end of verification
and additionally that all message queues are empty use the -q with
the compiler verifier.
Progress (Liveness) States
Used to specify livenesss properties.
Similar syntax to end states but use labels with the prefix progress to mark
statements that accomplishes something - allows infinite cycles to be seen as "good"
rather than an error condition that signals that a process is stuck making no progress.
See the SPIN command line usage on how to search for no-progress cycles. Enabling NP searching disables the search for invalid end states (safety).
Faireness
Every process that can execute a statement will eventually do so. I.e., no starvation. There are two types of faireness: weak and strong faireness.
[Weak fairness] states that if a process reaches a point where it has an executable statement, and the executability of that statement never changes, it will eventually proceed by executing the statment...
...[Strong faireness] states that if the process reaches a point where it has a statement that becomes executable intinitely often, it will eventually proceeed by executing the statement.
See the SPIN command line usage on how enforce weak fairness. This adds a computational burden to the verification so it will be slower. Strong fairness no supported as too computationally expensive.
Accept States
Mostly used with a never claim. Used to find execution paths that do pass
through at least one accept state(s) but not infinitely often - use label prefix accept.
Never Claims
Claims that apply to every state in the entire system and all times, i.e.
at every execution step of the system
.
Ignored in simulation mode. Only used in verification mode. Help capture liveness requirments.
Example of checking system invariant p, taken from "The SPIN Model Checker, Primer and Reference Manual" by G. J. Holzmann.
never {
do
:: !p -> break /* } Replace both lines with assert(p) */
:: else /* } for equivalent behaviour */
od
}
If the invariant is ever broken, i.e. !p, the never claim exits,
which signals to SPIN that a violation has occured. Expressions in the claim must be
side effect free!
Note the use of else. As the claim is to be checked at each statement
execution the loop must not block, although it is permissible for never claims
to block.
A more comples example from "The SPIN Model Checker" book (annotation mine):
/* CHECK that every state in which p is true eventually leads to a state
* in which q is true, and in the interim, p remains true.
*
* SPIN checks for VIOLATIONS of this property only (i.e., does not check
* satisfaction).*/
never {
S0: do
:: p && !q -> break /* p is true AND q is false -> expect q to become true */
:: true /* Always executable, which is how we get the... */
od /* ..."eventually leads to a true " because even... */
/* ...when (p &&!q) is true, this branch could... */
/* ...execute instead. Also allows for p to go false */
/* ... and then true again before we hit our condition.*/
S1:
accept: /* Remaining in this loop is a valid end state */
/* The loop blocks when p and q true in this accept state and the claim STOPS... */
/* ...tracking system execution - we don't have to create another infinite accept...*/
/* ...state */
do
:: !q /* p is any AND q is false **forever**. Must mark as...*/
/* ... valid end state, otherwise q never becoming... */
/* ... true would be an error! */
:: !(p || q) -> break /* p is false AND q is false -> true p did not reach...*/
/* ...a true q! */
od
/* The loop will exit (and cause a claim violation) if !p && !q */
}
To generate a never claim you can use the spin command line: spin -f 'ltl-formula'.
You can make life a little easiler for yourself by combining complex expressions into #define'd
symbols. For example, in one simulation I wanted to chech that the following would always be
true: !(lock_grant[0] && lock_grant[1]) && !(bus_connect[0] && bus_connect[1]) && (!bus_connect[0] || lock_grant[0]) && (!bus_connect[1] || lock_grant[1]) && (num_connected < 2). I also wanted to make sure that the following
would be eventually true: (lock_grant[0] && bus_connect[0]) and
seperately, (lock_grant[1] && bus_connect[1]).
All of this would be a bit of a mouthful to have to type into the command line. So, instead, in the model:
#define always_c (!(lock_grant[0] && lock_grant[1]) && !(bus_connect[0] && bus_connect[1]) && (!bus_connect[0] || lock_grant[0]) && (!bus_connect[1] || lock_grant[1]) && (num_connected < 2)) #define eventual_co1 (lock_grant[0] && bus_connect[0]) #define eventual_co2 (lock_grant[1] && bus_connect[1])
Then, generating the never claim was done like so: spin -f '([]always_c) && (<>eventual_co1) && (<>eventual_co2) */
T'. Much easier :)
It is also possible to use the ltl section directly in your models:
ltl my_model_condition_1 {
([]always_c) && (<>eventual_co1) && (<>eventual_co2)
}
Trace Assertions
Used for message channels. All referenced channels must be global and all choices must be deterministic.
An example from the SPIN book:
trace {
do
:: q1!a; q2:b /* Says all ops on queue q1 must be send a, receive b, repeat */
od
}
A trace assertion can only use simple queue operations. Values matched must
be constants or mtype or the special variable _, which means
"don't care ".
Use notrace blocks to achieve the exact opposite.
SPIN Command Line
Limit Simulation Steps
The following limits the simulation exection to n steps:
spin -u<n> file.pml
For example, to limit it to 50 steps we would write:
spin -u50 file.pml
Columnated Output
To just get the prinf output, one column per process:
spin -c file.pml
Generate Verification model
spin -a filename.pml cc -o pan pan.c ./pan
If there are any errors a trail file will be output named
filename.pml.trail.
The shorthand for the above is to run the following.
spin -run filename.pml
Find Shortest Execution Trace
If a tail fails in <n> steps, to find the shortest
possible path to failure less than or equal to n steps:
spin -a file.pml cc -DREACH -o pan pan.c ./pan -i -m<n>
Alternatively compile to use breadth first search:
cc -DBFS -o pan pan.c ./pan
A shortcut for this should be the following.
spin -run -bfs file.pml
Guided Simulation (Use A Trail File)
To replay a trail file in a simulation:
spin -p -t file.pml
^ ^
^ -t is a trail-hunting option. If the analyzer finds a violation of an
^ assertion, a deadlock or an unspecified reception, it writes an error
^ trail into a file named pan.trail. The trail can be inspected in detail
^ by invoking Spin with the -t option. In combination with the options pglrs
^ different views of the error sequence are then easily obtained.
^
-p Shows the state changes of the Promela processes at every time step.
Or...
spin -p -replay file.pml
The pglrs options are:
| Option | Description |
-p |
Shows the state changes of the Promela processes at every time step. |
-g |
Shows the current value of global variables at every time step. |
-l |
Shows the current value of local variables, after the process that owns them has changed state. It is best used in combination with option -p. |
-r |
Shows all message receive events. It shows the process performing the receive, its name and number, the source line number, the message parameter number (there is one line for each parameter), the message type and the message channel number and name. |
-s |
Shows all message send events. |
Stricter End States - Message Queues Must Be Empty
By defailt when verification ends all promela-processes must be in a valid end state but
the message queues do not have to be empty. To make this stricter and require that message
queues also be empty use the -q with the compiled verifier.
Search For No Progress Cycles
spin -a file.pml # Compile the verifier cc -DNP -o pan pan.c # Enable search for no-progress cycles. ./pan -l [-f] # Search for NP cycles. # ^^^^ # Enforce weak fairness (strong fairness too computationally expensive)
SPIN In Action
Playing with SPIN verification example exercise 3a:
This was my solution to the exercise...
bool yield[2];
int lock;
int cr_count = 0;
active [2] proctype mutex_proc()
{
int other_procno = 1 - _pid
C0: yield[_pid] = false
C1: if
:: lock != _pid ->
C2: if
:: !yield[other_procno] -> goto C2
:: else -> lock = _pid; goto C1
fi
:: else ->
CR: // Enter critical region
cr_count = cr_count + 1
// Do some critical stuff
// Leave CR
cr_count = cr_count - 1
yield[_pid] = true
// Remainder of program (out of CR)
goto C0
fi
}
never { /* <>(cr_count > 1) */
T0_init:
do
:: atomic { ((cr_count > 1)) ->
assert(!((cr_count > 1))) }
:: (1) -> goto T0_init
od;
accept_all:
skip
}Following the instructions, one can use a BFS to find the smallest number of steps in which the never claim is violated and it can be examined as so:
~/SPIN$ spin -p -replay ex_3a.pml starting claim 1 using statement merging ^^ yield = {0, 0}, lock = 0, cr_count = 0 1: proc 1 (mutex_proc:1) ex_3a.pml:22 (state 1) [yield[_pid] = 0] ^^ Proc 1 wants the lock 2: proc 1 (mutex_proc:1) ex_3a.pml:24 (state 2) [((lock!=_pid))] ^^ Proc 1 examines the lock variable. It does not have the lock! 3: proc 0 (mutex_proc:1) ex_3a.pml:22 (state 1) [yield[_pid] = 0] ^^ Proc 0 wants the lock 4: proc 0 (mutex_proc:1) ex_3a.pml:29 (state 10) [else] ^^ Proc 0 has the lock 5: proc 0 (mutex_proc:1) ex_3a.pml:31 (state 11) [cr_count = (cr_count+1)] ^^ yield = {0, 0}, lock = 0, cr_count = 1 6: proc 0 (mutex_proc:1) ex_3a.pml:34 (state 12) [cr_count = (cr_count-1)] ^^ yield = {0, 0}, lock = 0, cr_count = 0 7: proc 0 (mutex_proc:1) ex_3a.pml:35 (state 13) [yield[_pid] = 1] ^^ yield = {1, 0}, lock = 0, cr_count = 0. Proc 0 releases lock 8: proc 1 (mutex_proc:1) ex_3a.pml:27 (state 5) [else] ^^ Proc 1 can take the lock as proc 0 has yielded 9: proc 0 (mutex_proc:1) ex_3a.pml:22 (state 1) [yield[_pid] = 0] ^^ Proc 0 wants the lock. yield = {0, 0}, lock = 0, cr_count = 0 10: proc 0 (mutex_proc:1) ex_3a.pml:29 (state 10) [else] ^^ ERROR! Proc 0 thinks it has the lock! 11: proc 1 (mutex_proc:1) ex_3a.pml:27 (state 6) [lock = _pid] ^^ ERROR! Proc 1 thought it was clear to take the lock Proc 1 takes the lock: yield = {0, 0}, lock = 1, cr_count = 0 12: proc 1 (mutex_proc:1) ex_3a.pml:29 (state 10) [else] 13: proc 1 (mutex_proc:1) ex_3a.pml:31 (state 11) [cr_count = (cr_count+1)] 14: proc 0 (mutex_proc:1) ex_3a.pml:31 (state 11) [cr_count = (cr_count+1)] ^^ ERROR! Both proc 0 and 1 are in the CR! spin: trail ends after 14 steps #processes: 2 yield[0] = 0 yield[1] = 0 lock = 1 cr_count = 2 ^^ ERROR! The never claim is violated 14: proc 1 (mutex_proc:1) ex_3a.pml:34 (state 12) 14: proc 0 (mutex_proc:1) ex_3a.pml:34 (state 12) 14: proc - (never_0:1) ex_3a.pml:43 (state 6) 2 processes created
By examining the trace we can see why this algorithm has failed. When the lock is yielded, it is not set to a value that represented "not-owned", so proc 0 thought it had the lock, when in fact, no one had the lock!
The never claim, "" was generated using the command line spin -f "<>(cr_count > 1)"


