DSP Notes

Page Contents

References

None

To Read

https://www.maths.ox.ac.uk/system/files/attachments/complex%20%281%29.pdf
https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-i-first-order-differential-equations/complex-arithmetic-and-exponentials/MIT18_03SCF11_s6_5text.pdf
https://www.pearsonschoolsandfecolleges.co.uk/Secondary/Mathematics/16plus/EdexcelModularMathematicsforASandALevel/Resources/FurtherPureMathematics2/03%20Ch%2003_018-065.pdf
http://faculty.uml.edu/cbyrne/SP1text.pdf
http://www-math.mit.edu/~gs/papers/newsigproc.pdf
http://www.ling.upenn.edu/courses/ling525/Moore1978Part1.pdf
http://www.ling.upenn.edu/courses/ling525/Moore1978Part2.pdf
http://greenteapress.com/thinkdsp/thinkdsp.pdf
http://web.eecs.umich.edu/~aey/eecs206/lectures/phasor.pdf
https://www.gaussianwaves.com/2015/11/interpreting-fft-results-complex-dft-frequency-bins-and-fftshift/ << AWESOME
https://math.stackexchange.com/questions/9416/extracting-exact-frequencies-from-fft-output
https://dsp.stackexchange.com/questions/38577/fft-starting-at-zero

An Intro To Digital Signals

What Is A Digital Signal?

picture of sinc function
Digital means:
  • Discrete time
  • Discrete amplitude

Analogue and digital signals can carry the same information under certain conditions. Answered by Harry Nyquist and Claude Shannon. When the sampling frequency is at least double the maximum frequency in the signal being sampled, the sampling theoroem holds: x(t) = \sum_{n=-\infty}^{\infty} x[n] \mathrm{sinc}\left(\frac{t - nT_s}{T_s}\right) We can build the continuous time signal from the discrete time sequence. Take copies of the \mathrm{sinc}() function at each sample location scaled by the amplitude of the sample and sum them to get back the original function. The conditions under which you can do this are determined by the Fourier transform. Once we know the "speed" of the signal we can choose a sampling interval that will allow the above theorem to work - this is the Nyquist rate.

Discrete time signal is a sequence of complex numbers denoted x[n] where the square brackets are used to indicate its discrete nature. The index n just provides an ordering for samples which are taken at a steady interval, the sampling period. The sequence is two-sided in that it goes from minus infinity to plus infinity.

The delta signal: \delta[n] . TODO INSERT GRAPH

The unit step signal: \text{u}[n] . TODO INSERT GRAPH

The exponential signal: x[n] = |n|^nu[n], |a| < 1 . TODO INSERT GRAPH. E.g. describes newtons law of cooling or capacitor discharge.

The sinusoidal signal: \sin(\omega_0 n + \theta) . Angles in radians.

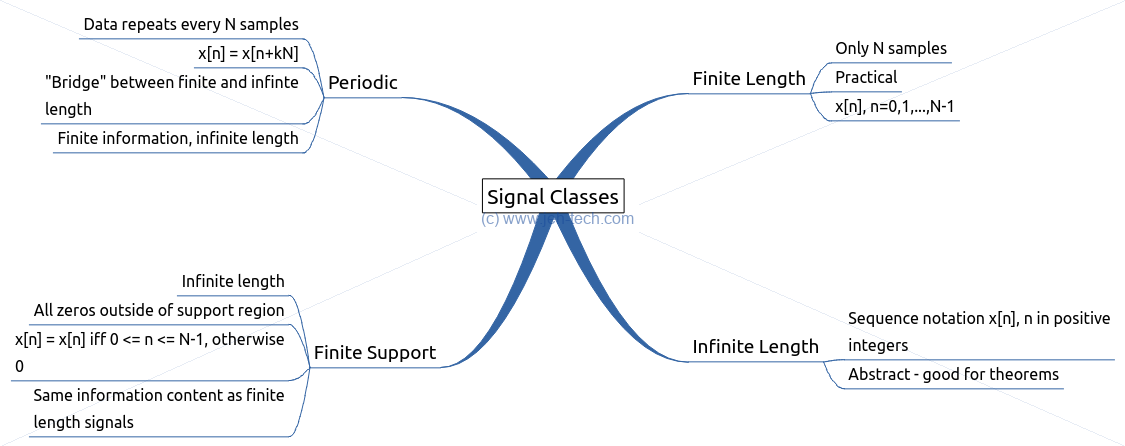
There are 4 signal classes:

  • finite length - only N samples. Range of index is 0 to N-1.
  • infinite length - index N ranges over entire range of integers. abstract. good for theorems. They have infinite energy.
  • periodic - data repeats every N samples. Represent with a tild on top. Same info as a finite-length of length N. They have infinite energy.
  • finite support - infinite length with on a finite number of non zero samples. Eg unit step.

Elementary Operations On Digital Signals

Elementary operations include scaling, sum, product and shift. These can be applied to any discrete signal.

  • Scale: y[n] = \alpha x[n],\ \alpha \in \mathbb{C} .
  • Sum: y[n] = x[n] + z[n] .
  • Product: y[n] = x[n] \cdot z[n] .
  • Shift: y[n] = x[n - k],\ k \in \mathbb{Z} .

Shift-by-k can be applied to infinite signals, but when applying to discrete time signals we need to state what happens when we go beyond the index range N, i.e., how we embed it into an infinite length sequence. Can embed into a finite-support sequence by putting zeros on the left and right. Or we could use a periodic extension, whereby the shift becomes circular. The periodic extension is the natural way to interpret the shift of a finite-length signal.

Energy And Power

Energy of signal defined by the following. E_x = \sum_{n = -\infty}^{\infty} |x[n]|^2

Power is the rate of energy production defined as follows. P_x = \lim_{N\to\infty} \frac{1}{2N+1} \sum_{n=-N}^{N} |x[n]|^2 It is like the overage energy over one period or energy per unit time.

Analog To Digital And Back Again

Analog signals are sampled at regular intervals to produce digital signals. The time between samples is called the sampling period and is detoted T_s .

If x_a(t) is our analog signal, that we sample with period T_s , then our sampled signal x[n] is related to the anlog by: x[n] = x_a(nT_s) The sampling period is just F_s = 1/T_s .

There is thus the following relationship between discrete samples and anlalog time: t = nT_s = \frac{n}{F_s}

Therefore, if a signal has a period of M samples then this period is MT_s seconds long, which means that the original signal in the analog world had a frequency of f = \frac{1}{MT_s} \text{Hz} .

For example, a typical sampling frequency for audio is T_s = 48000\text{Hz} and therefore the sampling period is T_s \approx 20.8\mu\text{S} .

In this case, if we know that there are 110 samples in the signal's period, i.e. M=110 , we can say that the frequency of the signal is f \approx 440Hz .

Discrete Time Sinusoids Not Always Periodic

A discrete complex exponential is only period if the frequency is a rational number (any number that's a fraction p/q of two integers) of 2\pi .

I.e., to be periodic the frequency must satisfy: \omega = \frac{M}{N}\cdot 2\pi\ m,n \in \mathbb{N} To be periodic recall that x[n] = x[n + N] . This means that: \begin{align} e^{j(\omega n + \theta)} &= e^{j(w(n + N) + \theta)} \\ &= e^{j(\omega n + \omega N + \theta)} \\ &= e^{j\omega n} e^{j\omega N} e^{j\theta} \\ \therefore e^{j\omega n} e^{j\theta} = e^{j\omega n} e^{j\omega N} e^{j\theta} \end{align} The only way this can be true is if e^{j\omega N} , which can only be true if \omega N = 2M\pi and thus if \omega = 2\pi \frac{M}{N} .

The fundamental frequency is the smallest value of N for which x[n] = x[n + N] is true.

Aliasing

Discrete time sinusoids whos frequencies are separated by an integer multiple of 2\pi are identical, as shown in the reasoning above.

This gives rise to something called aliasing, where any discrete time sinusoid has multiple equivalends, or aliases, separated by integer multiples of

DFT/FFT

\text{binResolution} = \frac{f_\text{sample}}{\text{# FFT points}} \begin{align} \mathrm{binStartFreq}(n) &= n * \text{binResolution} \\ &= n \frac{f_\text{sample}}{\text{# FFT points}} \end{align} 

http://www.tedknowlton.com/resume/FFT_Bin_Interp.html
https://electronics.stackexchange.com/questions/12407/what-is-the-relation-between-fft-length-and-frequency-resolution