Electronics Notes...
Page Contents
Charge, Current, Voltage
References
- The Great Power vs. Energy Confusion, Rob Lewis.
- Electric potential energy, Khan Academy.
- Essential & Practical Circuit Analysis: Part 1- DC Circuits, Solid State Workship, YouTube.
Conventional Current And Charge
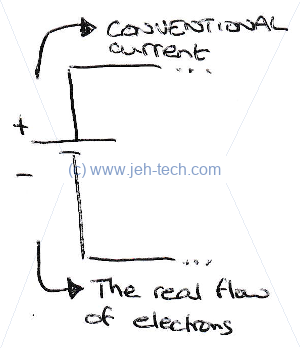 Historically positive charge moves through the circuit from the positive to negative terminals. This is called conventional current.
We now know that it is, in fact, the flow of electrons from the negative to positive terminals that is current. Due to the historical precedent,
current is still often shown as conventional current.
Historically positive charge moves through the circuit from the positive to negative terminals. This is called conventional current.
We now know that it is, in fact, the flow of electrons from the negative to positive terminals that is current. Due to the historical precedent,
current is still often shown as conventional current.
From Wikipedia: Conventional current flows from the positive pole (terminal) to the negative pole. Electrons flow from negative to positive. In a direct current (DC) circuit, current flows in one direction only, and one pole is always negative and the other pole is always positive. In an alternating current (AC) circuit the two poles alternate between negative and positive and the direction of the current (electron flow) reverses periodically.
.
Note that voltages are relative, which is why the negative terminal of the battery can be negative - it depends what the reference voltage you are measuring agains is - e.g. if ground is midway between the two terminals then they will have voltages -A and +A respectively.
Informally, current is a flow of electric charge.
Current, , is the amount of charge, , that moves through a point in the circuit at any time. Charge, , is measured in Coulombs. One electron has a charge of Coulombs. This is the smallest unit of charge possible.
Voltage
Voltage, , is the amount of work (in Joules) that must be done per unit charge to move between two points in a field. I.e. 1 volt is 1 Joule per Coulomb.
To help understand this let's revisit the terms energy, work and power.
Energy is the ability to do work.
Work is the force that must be exerted to move a mass a certain distance.
Power is the rate at which energy is generator/consumed.
Energy is what makes it possible to move things. Moving things involves doing work and it takes energy to do this. Energy measures the total amount of work done. It does not say how fast the energy was used/produced.
Power gives that rate at which energy is used/produced. Power measures how fast the work gets done.
Give these definitions we can see how they are defined for electronics. Using some crude (read incorrect as we're using multiplcation not integration to make it seem simpler) we see: So energy is indeed the total work required to move a charge between two points in an electric field. And because We can see that electrical power (measured in Watts) is the rate of consumption/generation of electrical energy.
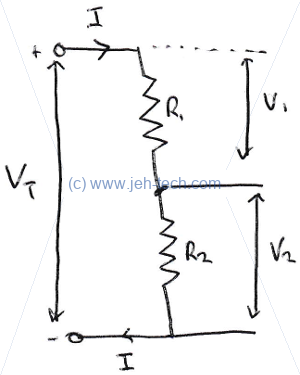
Note that electric potential energy is measured with respect to a reference point. In the image below one can see that the voltage either side of the resistor is measured w.r.t ground. Ground is the normal reference point, but any point in a circuit can be used as long as it is used consistently.
Note then, that potential difference, is the difference between to points, each of which has a potential energy w.r.t to a reference. The potential difference is the difference between these two points, but only make sense if the potential of each point is measured w.r.t to the same reference.
Ohm's Law
Ohm's law gives the relationship between voltage, current and resistance:
Kirchoff's Laws
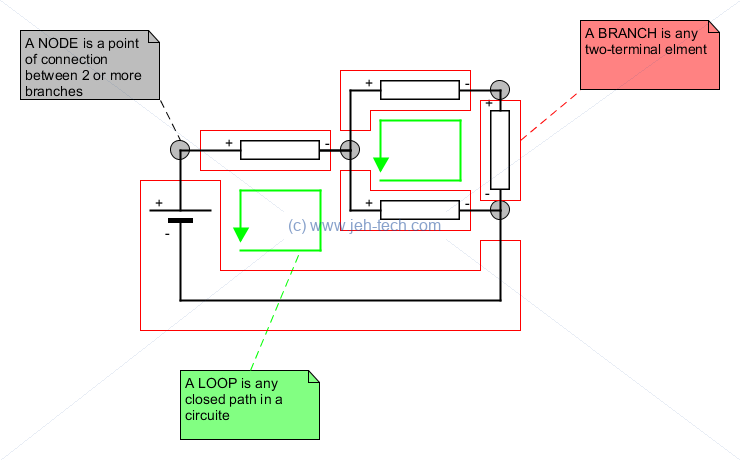
Nodes, Branches and Loops
Branch: A branch represents a single element such as a resistor. I.e., any two terminal element.
Node: A node is the point of connection between 2 or more branches. Every point going into the node, at the node, is at the same potential.
Loop: A loops is any closed path in a circuit. Starts and ends at the same node and does not pass through a node more than once.
The Laws...
Two important laws: Kirchoff's voltage law and Kirchoff's current law.
KCL
Kirchoff's current law says that the sum of currents flowing into a node must equal the sum of currents leaving a node. This is often expressed in another way: the sum of currents entering and leaving a node must always be zero. This works because we label, by convention, all currents entering the node as positive and all currents leaving the node as negative.
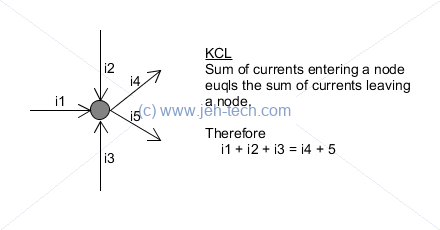
This can be written most compactly as:
Lets look at the following example [Ref]:
KVL
Kirchoff's voltage law says that the sum of voltages around a closed circuit must be zero.
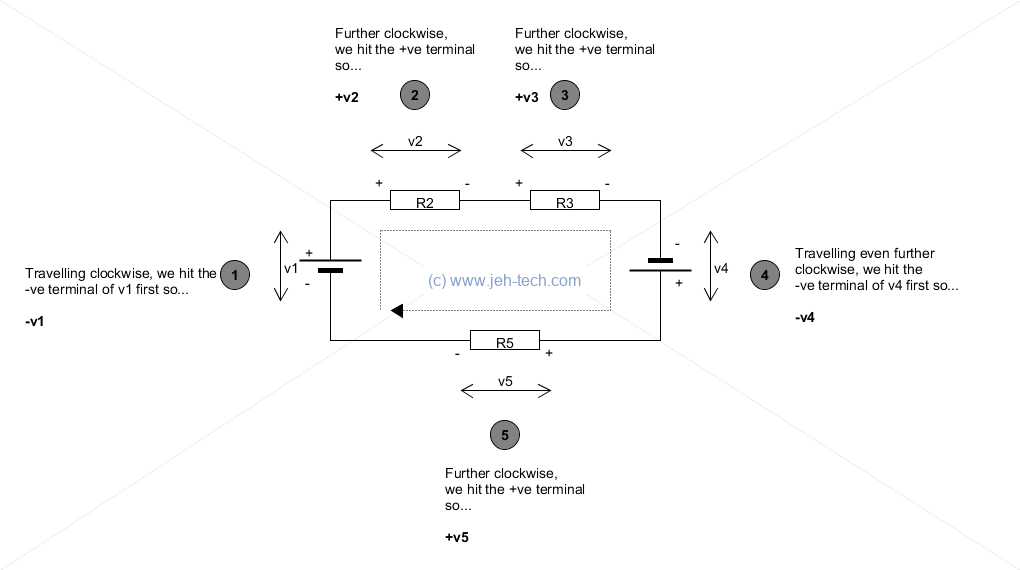
This can be written most compactly as:
Say, for example, that is 12V, R2 is , R3 is , is 3V and R5 is . Then we know . We can then work out the current in the circuit using KVL by re-arranging the formula.
Resistance
Resistors control the current that flows through a part of a circuit, as described by Ohm's Law (). Using the formula one can see that as either resistance increases, current falls, and vice versa.
Resistor Colour Codes
In the drawing to the left you can click on the value-boxes to change the colour bands on the resistor to find out the resistance represented by the colour encoding. Note it only shows a 4-band resistor. 5 and 6 colour bands are possible but not shown here.
Note: Sometimes the click event on the canvas doesn't fire... not quite sure why that is. If first click doesn't work, persevere :)
Some popular ways of remembering the resistor colour codes include "Bad Boys Ravish Our Young Girls But Violet Gives Willingly" and my fav, "Bad Booze Rots Our Youg Guts, But Vodka Goes Well".
Resistor's In Series
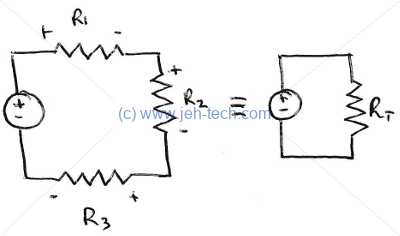
Resistors in series can be "collapsed" into an equivalent single resistor with a resistance that is the sum of all the resistances of the individual resistors.
Using Kirchoff's voltage law: Using we can substitute in for the individual voltages across each resistor. Note that because this is a closed loop the current though each resistor will be the same (as there is no path in which the current can "split" up). Now, can also be re-written using as , where is the equivalent, total, resistance of the resistors in series...
Resistor's In Parallel
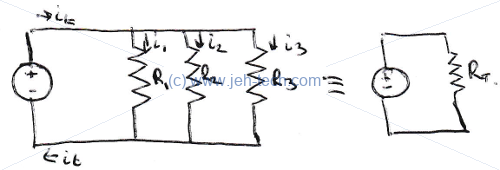
Resistors in parallel can also be "collapsed" into an equivalent single resistor...
Using Kirchoff's current law we can say that . Using , we can say the following: Subsituting the above back into , gives us the following. And, of course, can also be re-written, giving the solution:
Voltage Divider
Current Divider
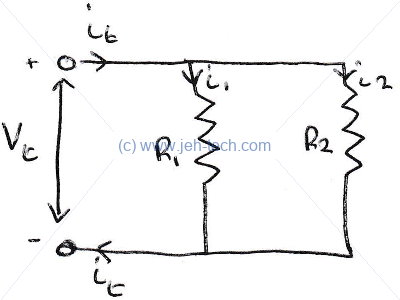
The Wheatstone Bridge
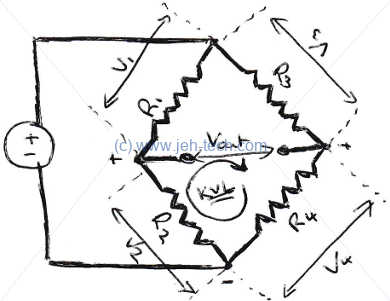
The Wheatstone Bridge is a circuit for measuring resistance very accurately. This material is based on the link to the Texas Instrument tutorial...
Using Kirchoff's voltage law around the loop consisting of , and we get the following. We can find the voltage across and by using the formula for voltage dividers: and are one voltage divider and and are the other voltage divider. Using the voltage divider formula we get the following two results: Here is the supply voltage. Substituting these into the first formula we get... If three out of the four resistances are known and the current across the branch is zero, the third resistance can be calculated.
Let's say that we don't know the resistance of . If we set all the other resistors to be equal so that , then the above formula simplified to the following.... Where is the known resistance and is the unknown resistance. This assumes that is roughly equal to and that all resistors are very closely matched.
A simple re-arrangement gives us...
In the above, , , and are all known. We know because we can measure it and the other known parameters are already set apriori. With more simple re-arrangement we get...
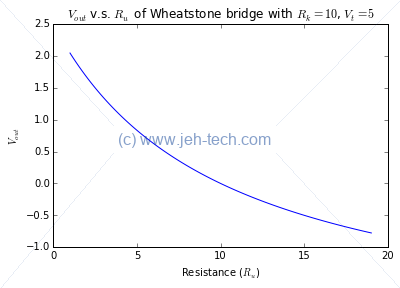
And now we can calculate the unknown resistance... why is this useful? Because this unknown resistance is our sensor. It could be a thermistor, LDR, or whatever... something that changes resistance due to the thing we're trying to measure.
One thing to note is that the of the Wheatstone Bridge is non-linear as the figure to the left shows: does not change linearly with changes in the unknown resistance ! In the figure I just picked pretty arbitrary values for the various knowns.
So... why use this rather complex arrangement to measure an unknown resistance when we could do the same using a simple voltage divider? The answer lies in the sensitivity of the measurement system. This is covered in the next section.
Power
When current flows through a resistor it disipates power in the form of heat. When it flows through an LED it disipates power in the form of both heat and light.
Power, measured in watts, is defined as:
Resitors usually have a power rating (the power they can disipate) associated with them. This means that if you know the resistor's power rating you can calculate the maximum voltage or current you can put across/through them without breaking the resistor.
Voltage Sources & Current Sources, Ideal v.s. Real World
Voltage Sources
An ideal voltage source is one that supplies constant potential, no matter what load is connected to it. I.e., it produces whatever current is necessary to maintain the voltage across it [Ref]:
But, batteries, even power supplies etc etc are not ideal. In the real world they have a small internal resistance, anywhere between approx 0.1 Ω to 2 OHM() depending on the battery [Ref], which means they are modelled more like this:
It can be seen that because the internal resistance of the battery, is in series with the circuit it is powering, i.e., the load (simulated by the resistor), the combination acts like a voltage divider, and so the voltage across the load varies with its resistance. I.e.,the battery is not ideal (but its pretty close!)
This is why it is always best to measure the voltage across a power supply when it is under load.
We can now also understand that an ideal voltage source is one that has zero internal resistance.
Current Sources
An ideal current source is one that always produces the same current, no matter how the voltage across it or the resistance of the load it is "feeding" varies, [Ref].
This is why, incidently, in a circuit you cannot have two current sources in series!
Source Transformations
It is possible to switch out a voltage source in a circuit for a current source and vice-versa using source transformation using Thevenin and Norton equivalent ciruits [Ref].
Superposition
Circuits can have multiple sources. In this case, to determine voltage levels at nodes, the principle of superposition can be used:
- Set all sources to zero except one,
- Solve the necessary currents and voltages using only that source,
- Repeat the above step for each source
- Add the circuit values together - "superimpose" them onto one another.
Take the following example [Ref]:
In the above diagram we get:
References
- What Exactly Is A Current Source?, StackOverflow.com.
- Battery Internal Resistance, LearningAboutElectronics.com.
- Essential & Practical Circuit Analysis: Part 1- DC Circuits, Solid State Workship, YouTube.
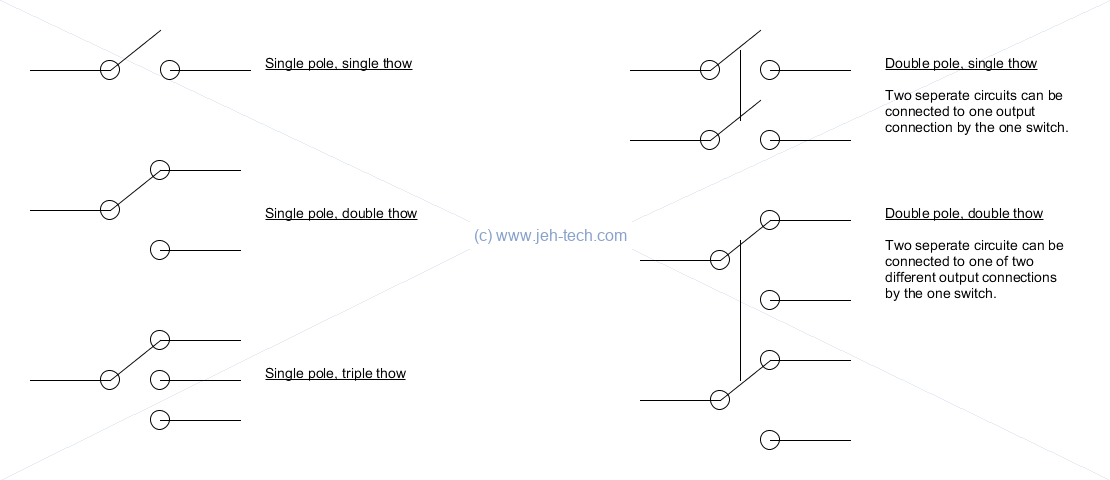
Switches
Switches are defined by the number of poles and throws they have...
Poles: A switch pole refers to the number of separate circuits that the switch controls.
Throw: The number of throws indicates how many different output connections each switch pole can connect its input to. Think of it as how many places a single source can be "thown to".
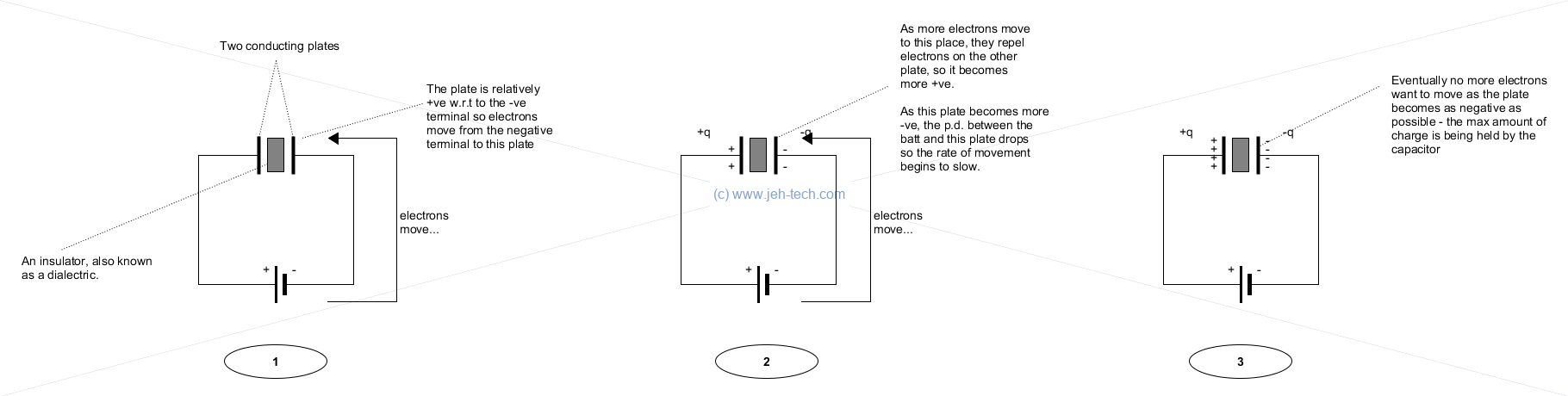
Capacitance
A capacitor consists of two conducting plates separated by an insulator (a.k.a. a dialectric).
When connected to a voltage source, the source creates a positive charge on one plate and a negative one on the other plate:
Charge stored is proportional to applied voltage: Where is called the capacitance of the capacitor and is measured in Farads (F). By re-arranging the above we can see that capacitance is the charge per volt that the capacitor can store. Thus, the more charge that the capacitor stores per volt, the higher its capacitance is. This quanitity is dependent on the type of dialectric used, the surface area of each plate and the distance between the plates.
Recall that current is the amount of charge that moves past a point per unit time. Thus, by differentiating w.r.t time, the above, we get the current-voltage relationship of a cap: This gives us in important property of caps. Because for DC current the voltage does not change, is zero, so a capacitor is an open circuit to DC! (But it does charge). Because of the definition of a derivative, we also know that the voltage across a cap must be smooth - i.e., it cannot change abruptly.
Note that real capacitors dissipate their energy over time - they "leak"
Capacitors resist abrupt changes in voltage, which is why the function as low pass filters.
Charging Through A Resistor
When a capacitor, with a capacitance , charges in series through a resistor of resistance ohms, in seconds it will charge to 63% of the supply voltage and in seconds it charges to over 99% [Ref]. You get an exponentially decreasing current flow as the resistor draws current from the battery and the capacitor stores the current's flowing charge [Ref].
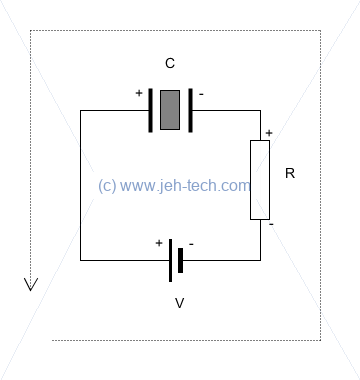
Recall KVL: the sum of voltages around a closed circuit must be zero. The dotted arrow in the diagram above shows a direction around a closed ciruit, which by KVL means that [Ref]: I.e., the current at time is proportional to the difference in voltages across the supply and the capacitor, the constant of proportionality being the resistance.
Now a quick aside to derive something we're going to need:
Recall: If we differentiate w.r.t time, we get: And we know that , so we can write: I.e., the current at time is also proportional to change in voltage across the capacitor, the constant of proportionality being the capacitance.
Now we can continue by substituting into to get: TODO - FILL REST IN
We end up with: We can see that as the value of RC increases, the exponential value will decrease, which means that the time it takes to charge the capacitor increases with either , or both of, and .
Capacitors In Series
Capacitors In Parallel
References
- Capacitor i-v equation in action, Willy McAllister, Khan Achademy,
- Derivation of Charging and Discharging Equations for RC Circuit, Khan Achademy,
- Deriving the formula from scratch for charging a capacitor, Adam Haun's answer on StackOverflow.com,
Inductors
An inductor is a coil of wire, sometimes round a feris core, that stores energy in its magnetic field. Its strength depends on the number of turns in the coil and the type of core material and its cross-sectional area.
Inductors oppose the change of current flowing though them. They are measured in "Henrys". The formula below defines inductance, L. Inductance is the voltage generated per unit change in current. Integrating both sides and re-arranging we can get:
Inductors In Series
Inductors In Parallel
So, for 2 inductors in parallel:
Diodes

Diodes let current flow in one direction, but not the other, and always drop the same voltage across them no matter the src voltage.
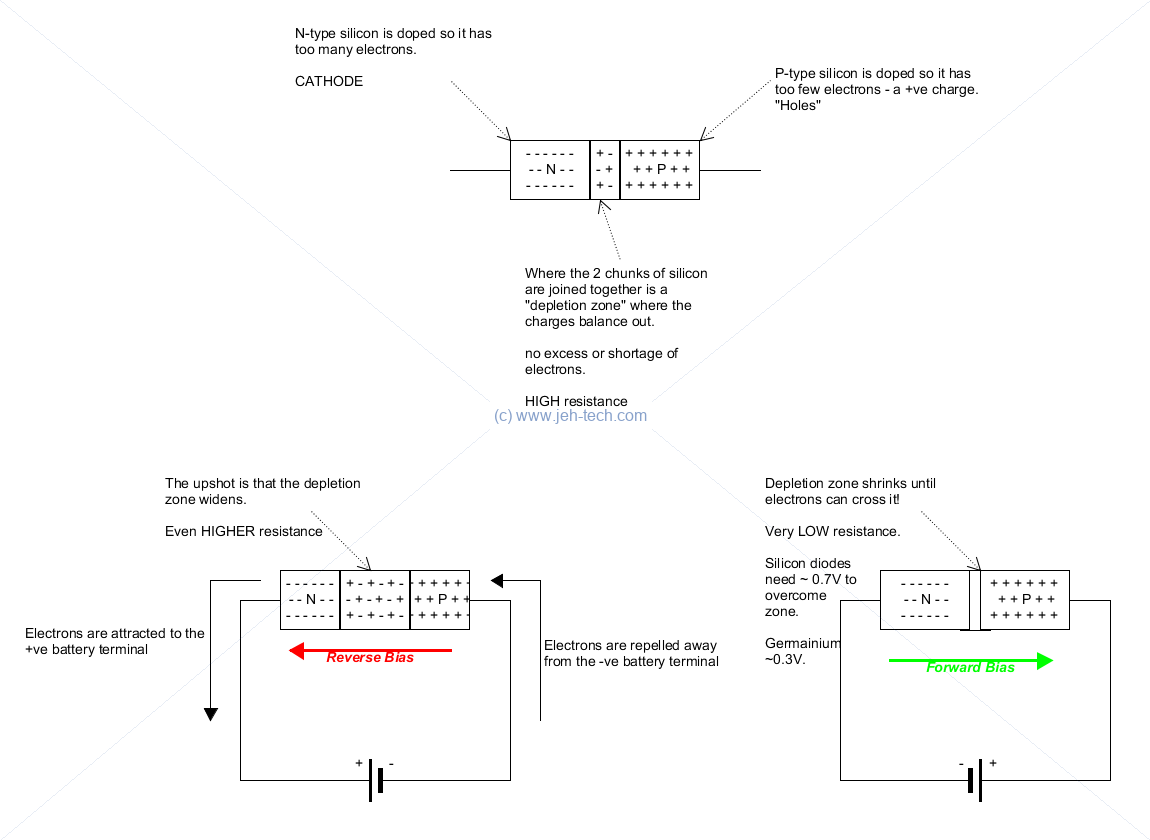
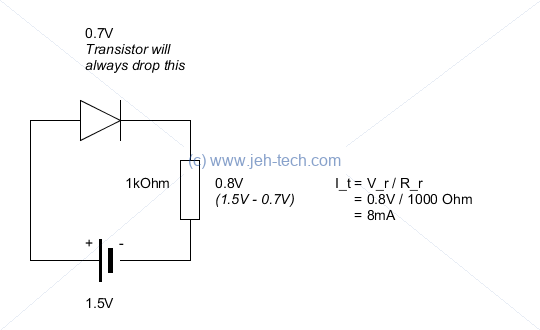
Diodes drop the same voltage across them no matter the voltage source rating. So, for example, silicon diode needs about 0.7V to fwd bias, but won't let the voltage drop across it exceed this. So if you don't protect it with a resistor it will allow too much current to flow an potentially overheat!
References
- Diodes and Diode Circuits.
- Accounting for LED resistance, StackExchange.
555 Timer
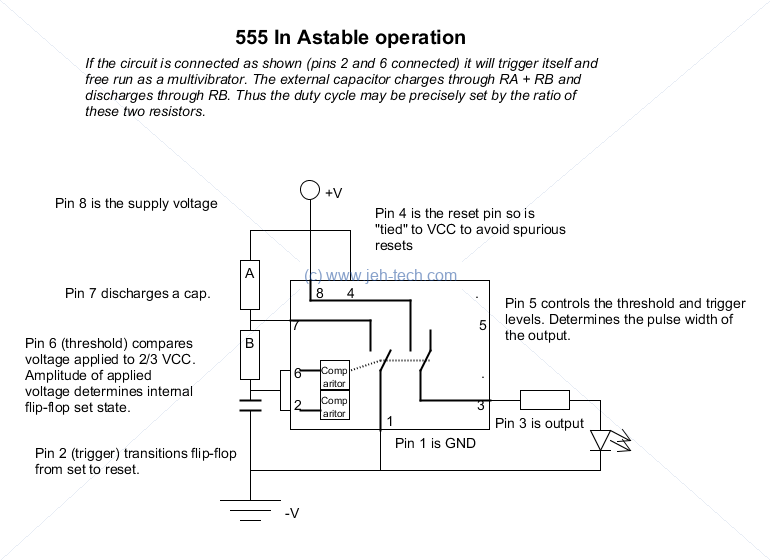
The total resistance RA + RB will determine the time it takes for the transistor to charge, assuming we keep capacitance constant. However, when the capacitor discharges, it only discharges through RB.
Recall charge time for a cap to charge to 63% of the voltage across is is . So by varying either the resistors or the capacitor the period of the pulse train output on pin 3 can be varied.
The diagrams above and below imagine that there is a switch inside the 555, which there is, its just not a mechanical switch like these diagrams suggest (see later below for more details). As the capacitor charges the voltage across it increases. When it hits 2/3 of the reference voltage, the switch in side the 555 closes such that pin 7 is shorted to ground. The capacitor then immediately starts to discharg through RB and when the voltage across the capacitor is less than 1/3 the reference voltage the switch opens again, starting the charge cycle and so on.
As the switch also controls the connection between the reference voltage and the output, this produces a pulse train who's frequency is determined by the two resistors and the capacitor, and with a duty cycle that is determined by the two resistors.
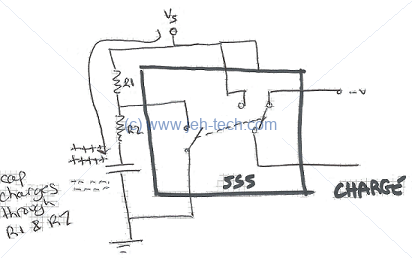

The following is a silly little animation of the capacitor discharging through R2. Imagine that the 3 red dots represent the flow of electrons from the negatively charged plate to the positive plate of the capacitor as it discharges. I think normally it would be shown using conventional current flow, but this animation uses actual electron flow. meh.
Wikimedia has a really nice illustration of the components in the 555, which I've copied below and inserted the components outside the chip that we used above to create an astable vibrator. Here, we can see that the switch shown above is really an RS flip flop combined with a transitor.
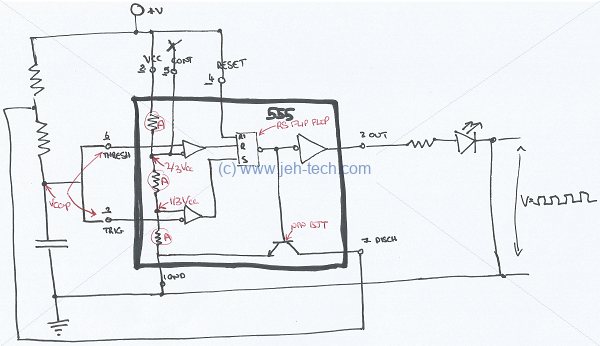
Each of the components, like the RS flip flop, comparitors and other gates can be further broken down into their transitor/resitor combinations, so the above is just another, slightly more detailed abstraction. The real circuit is far, far more complex when broken down into its "atomic" building blocks!
555 References
- 555 Timer IC - Working Principle, Block Diagram, Circuit Schematics, Dejan, Mechatronics How To.
- NE555 Block Diagram, BlanchardJ / Public domain.
- Sequential Logic Circuits, Electronic Tutorials, SR Flip Flop.
- NAND gate, WikiPedia.
Bipolar Junction Transistors (BJT)
NPN transistors consist of two N-type (negatively doped - excess electroncs) silicon "chunks" sandwiching a P-type (positively doped - exess holes or lacking electrons) as shown below. They are current controlled.
By forward biasing the emitter to base junction with even a small current, the transistor's resistance between the emitter and collector quickly decreses, allowing a relatively large current to from from the emitter to collector. I.e., base current controls current at emitter and collector.
The above configuration is called the common emitter configuration and is probably the most widely used [Ref].
NPN transistors can typically handle up to about 0.8 A. Thus, they are low current devices. For large currents MOSFETs are used (later section).
Saturation region is where the maximum collector current flows and the transistor is basically a closed switch from collector to emitter.
Active mode / region is where there is an almost linear relationship between the terminal currents at the base, collector and emitter. The transistor has some resistance, that is determined by the emitter/base current.
Cut-off region is where the transistor acts like an open switch.
A common NPN transistor is the 2N2222. Looking at the data sheet [Ref] we can find the following properties:
| Parameter | Max |
| Collector-base voltage VCBO | 60 V |
| Collector-emitter voltage VCEO | 30 V |
| Emitter-base voltage VEBO | 5 V |
| Peak collector current | 800 mA |
| Peak base current | 200mA |
| Total power disipation | 500 mW |
We can see that this device can handle a maximum of 0.8A though its emitter-collector and only 0.2A at the base. It is however, able to tolerate relatively high voltages, just not high currents, which as we said above, you'd need MOSFETs, or even relays for.
Lets represent the above common emitter example as a circuit diagram:

- The base is responsible for initiating transistor action. When a voltage is applied at the base, it gets biased and draws small current which is then used to control large current at the collector and emitter side.
- The base action is considered as an ON-OFF valve which generates current when a proper bias voltage is applied at this terminal.
- The small change at the voltage applied at the base terminal shows a large impact at the output terminals. Actually, base acts as an input and collector acts as an output in NPN transistor.
- In case of silicon transistor emitter-base junction draws voltage around 0.7 when there is no voltage at the base terminal, in order to initiate the electron action and put the transistor in running condition, the base voltage must be greater than 0.7 voltage in case of silicon transistor and 0.3 in case of germanium transistor.
References
- Electricity & Electronics - Robotics, Learn By Building, Ian Juby on Udemy.
- NPN Characteristic Curves.
- Introduction To The NPN Transistor, TheEngineeringProjects.com.
- Transistor Configurations: Circuit Configurations, Electronics-Notes.com.
- NPN Transistor 2N2222 DataSheet.
Metal Oxide Semiconductor Field Effect Transistor (MOSFET)