Statistics Notes

Page Contents

References and Resources

  1. "Introduction To Statistics", Thanos Margoupis, University of Bath, Peason Custom Publishing.

    A technical book but quite dry (as most statistics books are!)

  2. "An Adventure In Statistics, The Reality Enigma", Andy Field

    A very entertaining book that explains statistics in a really intuitive way and uses examples that are actually slightly interesting!

The following are absolutely amazing, completely free, well taught resources that just put things in plain English and make concepts that much easier to understand! Definitely worth a look!

  1. The amazing Khan Achademy.
  2. The amazing CK12 Foundation.

The Basics of Discrete Probability Distributions

Some Terminology

Variables...

Categorical Variable Discrete variable which can be one of a set of such as the anwer to a YES/NO question: the variable can be either YES or NO. Or the answer to a quality question where the choices are good, ambivalent or bad, for example.
Consistent estimator A consistent estimator is one that converges to the value being estimated.
Numerical Variable Has a value from a set of numbers. That set can be continuous, like the set of real numbers, or discrete like the set of integers.
Random Variable The numerical outcome of a random experiment. Discrete if it can take on more than a countable number of values. Continuous if it can take any value over an uncountable range.
I.D.D. A sequence or other collection of random variables is independent and identically distributed (i.i.d.) if each random variable has the same probability distribution as the others and all are mutually independent.
Qualitative Data Data where there is no measurable difference (in a quantitative sense) between two values (that makes sense). For example, the colour of a car. The car can be "nice" or "sporty", but we can't define the the difference in terms of a number like 4.83, for example.
Quantitative Data Data is numerical and the difference between data is a well defined notion. For example, if car A goes 33 MPG and care B does, 40 MPG, then we can say the difference is 7MPG.
Ordinal Data The value of the data has an order with respect to other possible values.

Populations and samples...

It is always worth keeping in mind that probability is a measure describing the likelihood of an event from the population. It is not "in" the data set (or sample) obtained... a sample is user to infer a probability about a population parameter.

Population The complete set of items of interest. Size is very large, denoted N, possibly infinite. Population is the entire pool from which a statistical sample is draw.
Sample An observed subset of the population. Size denoted n.
Random Sampling Select n objects from population such that each object is equally likely to be chosen. Selecting 1 object does not influence the selection of the next. Selection is utterly by chance.
Parameter Numeric measure describing a characteristic of the population.
Statistic Numeric measure describing a characteristic of the sample. Statistics are used to infer population parameters.
Inference The process of making conclusions about the propulation from noisy data that was drawn from it. Involves formulating conclusions using data and quantifying the uncertainty associated with those conclusions.

Experiments...

Random Experiment Action(s) that can lead to \ge 2 outcomes where one cannot be sure, before performing the experiment, what the outcome would be.
Basic Outcomes A possible outcome from a random experiment. For example, flipping a coin has two basic outcomes: heads or tails.
Sample Space The set of all possible basic outcomes (exhaustively) from a random experiment. Note that this implies that the total number of possible outcomes is, or can be, known.
Event A subset of basic outcomes from a sample space. For example, a dice roll has 6 basic outcomes, 1 through 6. The sample space is therefore the set {1, 2, 3, 4, 5, 6}. The event "roll a 2 or 3" is the set {2, 3}.

Distributions...

Probability Mass Function (PMF) When evaluation a n function gives the probability that a random variable takes the value n. Only associated with discrete random variables. Also note that the function descibes the population.
Probability Density Function (PDF) Only associated with continuous random variables. The area between two limits corresponds to the probabilty that the random variable lies within those limits. A single point has a zero probability. Also note that the function descibes the population.
Cumulative Distribution Function (CDF) Returns the probability that X \le x .
Quantile The \alpha^{th} quantile of a distribution, F , is the point x_\alpha such that F(x_\alpha) = \alpha .

Population And Sample Space

We have said that the population is the complete set of items of interest.

We have said that the sample space is the set of all possible outcomes (exhaustively) from a random experiment.

So I wondered this. Take a dice roll. The population is the complete set of possible items {1, 2, 3, 4, 5, 6}. The sample space is the set of all possible outcomes, also {1, 2, 3, 4, 5, 6}. So here sample space and population appear to be the same thing, so when are they not and what are the distinguishing factors between the two??

The WikiPedia page on sample spaces caused the penny to drop for me:

...For many experiments, there may be more than one plausible sample space available, depending on what result is of interest to the experimenter. For example, when drawing a card from a standard deck of fifty-two playing cards, one possibility for the sample space could be the various ranks (Ace through King), while another could be the suits (clubs, diamonds, hearts, or spades)...

Ah ha! So my population is the set of all cards {1_heart, 2_heart, ..., ace_heart, 1_club, ...} but the sample space may be, if we are looking for the suits, just {heart, club, diamond, spade}. So the population and sample space are different here. In this case the sample space consists of cards separated into groups of suites. I.e. the popultation has been split into 4 groups because there are 4 events of interest. These events cover the sample space.

In summary the population is the set of items I'm looking at. The sample space may or may not be the population... that depends on what question about the population is being asked and how the items in the population are grouped per event.

Classic Probability

In classic probability we assume all the basic outcomes are equally likely and therefore the probability of an event, A, is the number of basic outcomes associated with A divided by the total number of possible outcomes: \begin{align} P(A) &= \frac{\text{number of outcomes relevant to event A}}{\text{total number of outcomes}} \\ &= \frac{N_A}{N} \end{align} Each basic output is equally likely. And, note, here we are talking about outcomes in the population.

An example of the use of classical probability might be a simple bag of marbles. There are 3 blue marbles, 2 red, and 1 yellow.

If my experiment is to draw out 1 marble then the set of basic outcomes is {B1, B2, B3, R1, R2, Y1}. This is also the population! Also, note that the sample space isn't {B, R, Y} because we can differentiate between similar coloured marbles and there is a certain quanity of each.

So, what is the probability of picking out a red. Well, here N = 6 and N_A = 2 because there are 2 red marbles in the sack. Therefore the probability is: P(red) = \frac{2}{6} = \frac{1}{3}

What if my experiment is to draw 2 marbles from the sack? Now the set of all possible basic outcomes, if the order of draw was important would be a permutation. This means that if I draw, for example, R1 then B2, I would consider it to be a distinctly different outcomes to drawing B2 then R1. That means my population is:

Selection 1 Selection 2 Selection 1 Selection 2
B1 B2 B2 B1
B1 B3 B2 B3
B1 R1 B2 R1
B1 R2 B2 R2
B1 Y1 B2 Y1
B3 B1
B3 B2
B3 R1
B3 R2
B3 Y1
R1 R2 R2 R1
R1 B1 R2 B1
R1 B2 R2 B2
R1 B3 R2 B3
R1 Y1 R2 Y1
Y1 B1
Y1 B2
Y1 B3
Y1 R1
Y1 R2

Which is a real nightmare to compute by trying to figure out all the permutations by hand, and imagine, this is only a small set! Maths to the rescue...

\begin{align} Permutations &= {_{n}P_r} = \frac{n!}{(n-r)!} \\ &= {_{6}P_2} = \frac{6!}{(6-2)!} \\ &= \frac{6 \times 5 \times 4 \times 3 \times 2 }{4 \times 3 \times 2} \\ &= 6 \times 5 \\ &= 30 \end{align}

And that is how many permutations we have in the above table (thankfully!).

So, if my question is what is the probability of drawing a red then a yellow marble, my event space is the set {R1Y1, R2Y1}.
Thus, if we say event A is "draw a red then a yellow marble", P(A) = \frac{N_A}{N} = \frac{2}{30} = \frac{1}{15}

What if we don't care about the order. What is the probability of drawing a red and a yellow? I.e. we consider RY and YR to be the same event...

Our event space therefore becomes:
{R1Y1, R2Y1 Y1R1, Y1R2}.

Thus, if we say event A is "draw a red and a yellow marble", P(A) = \frac{N_A}{N} = \frac{4}{30} = \frac{2}{15}

We are essentially now dealing with combinations.

Therefore in the above table, where we see things like...

Selection 1 Selection 2
B1 B2
B2 B1

...we can delete one of the rows. The set of all basic outcomes therefore becomes:

Selection 1 Selection 2 Selection 1 Selection 2
B1 B2 B2 B1
B1 B3 B2 B3
B1 R1 B2 R1
B1 R2 B2 R2
B1 Y1 B2 Y1
B3 B1
B3 B2
B3 R1
B3 R2
B3 Y1
R1 R2 R2 R1
R1 B1 R2 B1
R1 B2 R2 B2
R1 B3 R2 B3
R1 Y1 R2 Y1
Y1 B1
Y1 B2
Y1 B3
Y1 R1
Y1 R2

Again a nightmare to figure out by hand, so maths to the resuce...

\begin{align} Combinations &= {_{n}P_r} = \frac{n!}{r!(n-r)!} \\ &= {_{6}P_2} = \frac{6!}{2!(6-2)!} \\ &= \frac{6 \times 5 \times 4 \times 3 \times 2 }{4 \times 3 \times 2 \times 2} \\ &= \frac{6 \times 5}{2} \\ &= 15 \end{align}

And, again, that is how many selections (not included the ones we've deleted using a strikethrough font) we have in the above table (thankfully!).

So, now we can't ask about drawing a red then a yellow marble anymore as order doesn't matter. We can ask about drawing a red and a yellow though. My event space is now the set
{R1Y1, R2Y1 Y1R1, Y1R2}
because I not longer care about order-of-draw... Thus, if we say event A is "draw a red and a yellow marble", P(A) = \frac{N_A}{N} = \frac{2}{15}

We have noted that in clasical probability that the various outcomes are equally likely. This means that from my bag of marbles am am equally likely to pick any marble. But what if this was not the case? What if the blue marbles are very heavy and sink to the bottom of the sack whilst the other marbles tend to rest on top of the blue marbles. We could hardly say that I am as likely to pick a blue as I am a red in this case. In this cas we cannot use classical probability to analyse the situation.

Relative Frequency Probability

Here the probability of an event occuring is is the limit of the proportion of times an event occurs in a large number of trials. Why the limit? Well, the limit would mean we tested the entire popultation. Usually, however, we just pick a very large n and infer the popultation statistic from that. P(event) = \lim \limits_{n \to \infty} \frac{n_A}{n} Where n_a is the number of exerimental outcomes relevant to event A, and n is the total number of outcomes.

So, for example, if we flip a coin 1000 times there are 1000 total number of outcomes. If we observed 490 heads and 510 tails we would have... \begin{align} P(head) &= \frac{490}{1000} &= 0.49 \\ P(tail) &= \frac{510}{1000} &= 0.51 \end{align}

If the coin was entirely fair then we would expect an equal probability of getting a head or a tail. Frequentist theory states that as the sample size gets bigger, i.e., as we do more and more coin flips, if the coin is fair the probabilities will tend towards 50%. So if we did 1,000,000 samples, for example, we might expect... \begin{align} P(head) &= \frac{500100}{1000000} &= 0.5001 \\ P(tail) &= \frac{499900}{1000000} &= 0.4999 \end{align} So... more samples, the closer our probability estimate is to the real probabilities for getting a head or tail. The limit of the probabilities as the sample size tends to infinitely will be exactly 50%. The "real" is the probability from the population. Anything less is a sample of the population.

As n tends to infinity, we can say that n tends towards the popultation size, and then at this point you will arrive back at the formula for conditional probability you saw in the previous section

Event A OR Event B

A and B are independent: P(A \cup B) = P(A) + P(B)
A and B are not independent: P(A \cup B) = P(A) + P(B) - P(A \cup B)

What is independence? A and B are said to be independent if information on the value of A does not give any information on the value of B, and vice versa.

We can visualise this as follows, using a Venn diagram...

Venn diagram of probability for A and B and A or B when events are independent

If two events are independent then we can see that none of the basic outcomes from either event can occur for the other. Therefore, using either classical or relative-frequency probability we can see that P(A \cup B) = P(A) + P(B) .

Venn diagram of probability for A and B and A or B when events are dependent

Now the two events are related. They are no longer independent because some of the basic outcomes from one event are also basic outcomes of the other. Thus we can see that if we sum the probabilities for the basic outcomes for each, we will count the shared basic outcomes twice!

If that's not clear, think of it this way...

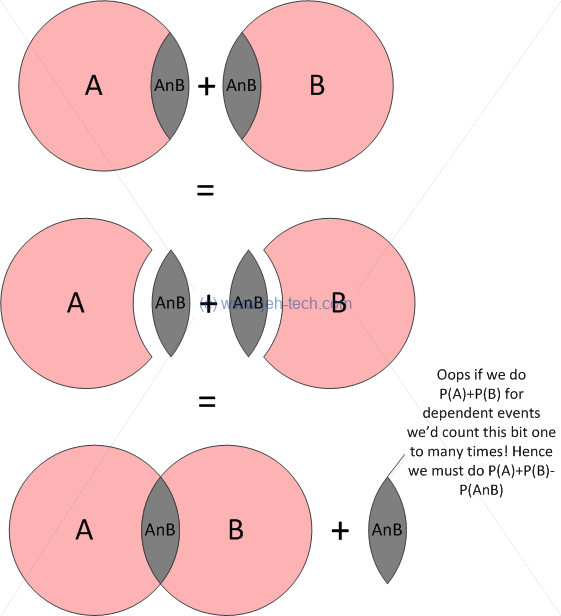
Event A AND Event B

We just talked about independence, but how do we know if an event A, is independent of another event, B? The answer is that two events are indpendent if P(A \cap B) = P(A)P(B) .

Why is this? Let's think of this from the relative frequency point of view. We know that P(A) = n_a/n and that P(B) = n_b/n for the sample and as n tends to infinity for the population.

For every basic outcome in the set A, we can pick an outcome from the set B, so the count of the combination of all possible outcomes from both sets must be n_a \times n_b . But this only makes sense if the events are mutually exlusive (i.e., don't overlap). P(A)P(B) = \frac{n_a \times n_b}{n} (See the previous figure of a Venn Diagram for two independent events to make this more clear in your mind).

So, what if the events are not independent? Then it is no longer true that the count of combination of all possible outcomes is n_a \times n_b . Why is this? This is because the events that can be in both A and B now represent a much smaller portion of sample space. The probability that A and B occur is now the solid-gray shaded area of the Venn diagram for dependent events.

Think if it this way. For A and B to both occur, at least one must have occurred, so now the only possible choices from the other event are in the overlapping region, not in the entire event space. Keep reading the next section on condition probability to find out more about why this is an indicator of independence.

A \overline A
B A \cap B \overline A \cap B \Sigma = P(B)
\overline B A \cap \overline B \overline A \cap \overline B \Sigma = P(\overline B)
\Sigma = P(A) \Sigma = P(\overline A) \Sigma = 1

Event A GIVEN Event B

If I live with my partner it seems intuitively correct to say that the probability of myself getting a cold would be heightend if my partner caught a cold. Thus there is an intutive difference between the probability I will catch a cold and the probability that I will catch a cold, given my partner has already caught one.

This is the idea behind conditioning: conditioning on what you know can change the probability of an outcome with no apriori knowledge of the data.

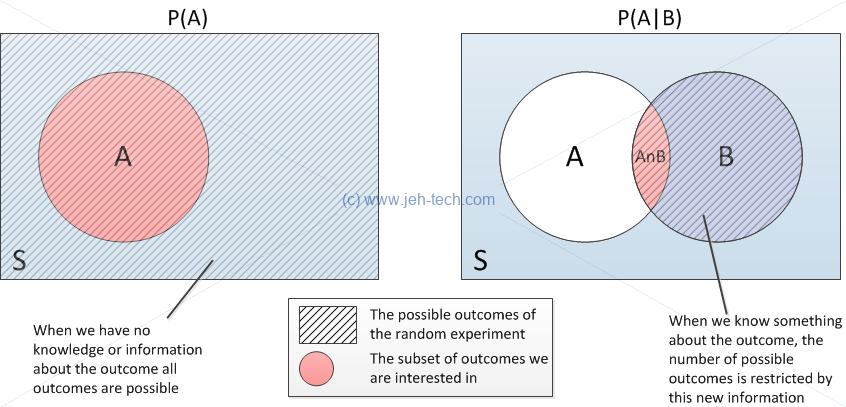
Conditional probability venn diagram

Lets look at a really simple example. I roll a dice... what is the probability that I roll a 3. We assume a fair dice, so the answer is easy: 1/6. The set all of basic outcomes was {1, 2, 3, 4, 5, 6} (the sample space) and only one outcome was relevant for our event... so 1/6.

Now lets say I have rolled the dice and I have been informed that the result was an odd number. With this knowledge, what is the probability that I rolled a 3? The set of basic outcomes is now narrowed to {1, 3, 5} and so the probability is now 1/3!

The probability of event A given that event B has occurred is denoted P(A | B) and is defined as follows: P(A | B) = \frac{P(A \cap B)}{P(B)}, \text{when}\ P(B) \ne 0

This makes intuitive sense. If B has occurred then the number of outcomes to "choose" from is represented by the circle for B in the Venn diagram below. The number of of outcomes that can belong to event A, given that we know event B has occurred, is the intersection. Therefore, our sample space is really now all the outcomes for event B, so n \equiv n_b , and the event of interest for A is now restricted to n_{a \cap b} . So we get... P(A | B) = \frac{n_{a \cap b}}{n_b} = \frac{\frac{n_{a \cap b}}{n}}{\frac{n_b}{n}} = \frac{P(A \cap B)}{P(B)}

If A and B are independent then clearly, because n_{a \cap b} = 0 , P(A | B) = 0 .

We can re-arrange the above to get another formula for P(A \cap B) ... P(A \cap B) = P(A | B)P(B)

And now we can see why, if two events are independent that P(A \cap B) = P(A)P(B) ... because when A and B are independent P(A | B) \equiv P(A) !. And when they are dependent that equality is not true.

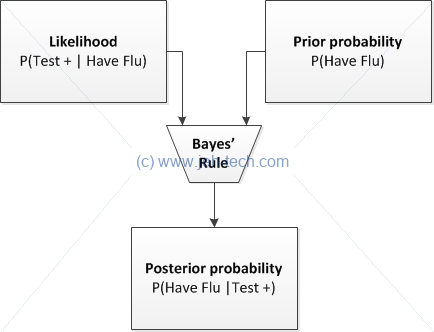
A small bit on terminology... P(A) is ofter called the prior probability and P(A | B) the posterior probability.

...A posterior probability is the probability of assigning observations to groups given the data. A prior probability is the probability that an observation will fall into a group before you collect the data. For example, if you are classifying the buyers of a specific car, you might already know that 60% of purchasers are male and 40% are female. If you know or can estimate these probabilities, a discriminant analysis can use these prior probabilities in calculating the posterior probabilities.
-- Minitab support

From the definitions so far we can also see that P(A | B) + P(\overline A | B) = 1 But that the following does not (necessarily) equal 1, P(A | B) + P(A | \overline B) \ne 1

Why is this important? Let's look at a little example. Say we have a clinical test for Influenza. Imagine that we know that for a patient the probability that they have or do not have Influenza. P(Flu) = 0.05 \implies P(\overline{Flu}) = 0.95

Any clinical test is normally judged by it's sensitivity and specificity. Sensitivity is the probability that the test reports infection if the patient has Influenza (i.e true positives). Sepcificity is the probability that the test reports the all-clear if the patient does not have Influenza (i.e., true negatives).

Let's say the test has the following sensitivity and specificity respectively: \begin{align} P(+ | Flu) &= 0.9 \\ P(- | \overline{Flu}) &= 0.9 \end{align} Because we know P(A | B) + P(\overline A | B) = 1 , we can say: \begin{align} P(- | Flu) &= 0.1 \\ P(+ | \overline{Flu}) &= 0.1 \end{align} But a clinitian wants to know the probabilities the other way around. The clinician will ask "if my patient has the flu, what is the probability that the test will call a positive?" I.e., the clinician wants to know P(Flu | +)

We can use the conditional probability formula to work this out... \begin{align} P(Flu | +) &= \frac{P(Flu \cap +)}{P(+)} \\ &= \frac{P(+ \cap Flu)}{P(+)} \end{align} We can find out P(+ \cap Flu) because P(+ \cap Flu) = P(+ | Flu)P(Flu) , which are quantities we already know, so we get... \begin {align} P(+ \cap Flu) &= P(+ | Flu)P(Flu) \\ &= 0.9 \times 0.05 \\ &= 0.045 \end{align} We're close, but what is the value for P(+) ? The answer is P(+) = P(+ \cap Flu) + P(+ \cap \overline{Flu}) : \begin{align} P(+) &= P(+ \cap Flu) + P(+ \cap \overline{Flu}) \\ &= 0.045 + ? \end{align} We still need to know P(+ \cap \overline{Flu}) . We know that P(+ \cap \overline{Flu}) = P(+ | \overline{Flu})P(\overline{Flu}) , and we know these quantities already, so: P(+ \cap \overline{Flu}) = 0.1 * 0.95 = 0.095 Therefore, P(+) = 0.045 + 0.095 = 0.14 Which means we can work out the entire thing (to 4dp): P(Flu|+) = \frac{0.045}{0.14} = 0.3214

Sensitivity v.s. Specificity

In clinical tests, the user often wants to know about the sensitivity of a test. I.e., if the patient does have the disease being tested for, what is the probability that that the test will call a positive results. Obviously, we would like this to be as close to 100% as possible!

The clinician would also like to know, if the patient did not have the disease, what is the probability that the test calls a negative. Again, we would like this to be as close to 100% as possible!

To summarise: sensitivity is the probability of a true positive, and specificity is the probability of a true negative.

Sensitivity: P(+ | D)
Specificity: P(- | \overline D)

Compliments

P(A \cup \overline A) = P(A) + P(\overline A) = 1\\ P(\overline A) = 1 - P(A)

Bayes' Theorem

Recall the multiplication rule: P(A \cap B) = P(A | B)P(A) = P(B | A)P(A) By re-arranging the above we can arrive at the following: P(A | B) = \frac{P(B | A)P(A)}{P(B)},\ \ \ P(B | A) = \frac{P(A | B)P(B)}{P(A)}

Because we know that P(B) = P(A \cap B) + P(\overline A \cap B) we could also write: P(A | B) = \frac{P(B | A)P(A)}{P(A \cap B) + P(\overline A \cap B)} An because we know P(A \cap B) = P(B | A)P(A) and P(\overline A \cap B) = P(\overline B | A)P(A) , we can re-write this as: P(A | B) = \frac{P(B | A)P(A)}{P(B | A)P(A) + P(\overline B | A)P(A)}

Remember that we called P(x) the prior probability. The prior is the probability distribution that represents your uncertainty over the random variable X. The posterior is the distribution representing your uncertainty after you have observed events that are related to or influence your event-of-interest: It is a conditional distribution, conditioning on the observed data. Bayes' theorem has given us a way to relate the two.

Flow diagram of Bayes Rule converting prior probability to posterior

Alternative Statement

This can sometimes be usefull re-stated as follows. If all events E_i are mutually exclusive and exhaustive and we have some other event A then we can write: P(E_i | A) = \frac{P(A | E_i)P(E_i)}{P(A)} And because in this case, \begin{align} P(A) &= P(A \cap E_1) + P(A \cap E_2) + \cdots + P(A \cap E_n) \\ &= P(A | E_1)P(E_1) + P(A | E_2)P(E_2) + \cdots + P(A | E_n)P(E_n) \end{align} We can say: P(E_i | A) = \frac{P(A | E_i)P(E_i)}{P(A | E_1)P(E_1) + P(A | E_2)P(E_2) + \cdots + P(A | E_n)P(E_n)} The advantage of this expression is that the probabilities involves are sometimes more readily available.

Discrete Probability Distributions

General Definitions

The Probability Mass Function (PMF) is another name for the Probability Distribution Function (PDF), P(x) , of a discrete random variable X expresses the probability that X takes the value x . I.e, P(x) \equiv P(X = x), \ \ \forall x The PMF has the following properties: 0 \le P(x) \le 1\, \ \forall x\\ \sum_x P(x) = 1

The Cumulative Mass Function (CMF) or Cumulative Probability Function (CPF), F(x_0) , for a random variable X , gives the probability that X does not exceed the value x_0 : F(x_0) = P(X \le x_0) = \sum_{x \le x_0} P(x) The CMF has the following properties: 0 \le F(X_0) \le 1, \ \ \forall x_0\\ x_0 \lt x_1 \implies F(x_0) \lt F(x_1)

Expected Value and Variance

Expected value defined as: E(X) = \mu = \sum_x xP(x) Where \mu is called the mean and is the mean of the population.

The calculation of measurements like E(X^2) becomes... E(X^2) = \sum_x x^2P(x)

Variance, \sigma^2 is the average squared distance from the mean and is defined as follows. The square is taken so that distances don't cancel eachother out (i.e, a negative distance and positive distance could result is a very small average distance, which is not what we want). \begin{align} \text{Var}(X) = \sigma^2 &= \sum_x (x - \mu)^2P(x) \\ &= E[(X - \mu)^2] \\ \end{align} We can re-write this as follows: \begin{align} \text{Var}(X) = \sigma^2 &= \sum_x (x - \mu)^2P(x) \\ &= \sum_x (x^2 - 2x\mu + \mu^2)P(x) \\ &= \sum_x x^2P(x) - 2\mu\sum xP(x) + \mu^2\sum P(x) \\ &= E[X^2] - 2\mu E[X] + E[X]^2 \\ &= E[X^2] - 2E[X]^2 + E[X]^2 \text{ , (because } \mu == E[X]\text{ and } \therefore \mu E[X] == E[X]^2 \text{)}\\ &= E[X^2] - E[X]^2 \end{align} In summary, \text{Var}(X) = E[(X - \mu)^2] = E(X^2) - \mu^2 = E(X^2) - E(X)^2

Standard Deviation, \sigma , is the positive square root of the variance.

The calculation of measurements like \text{Var}(aX) becomes... \begin{align} \text{Var}(aX) &= E[(aX)^2] - E[aX]^2 \\ &= E[a^2X^2] - (aE[X])^2 \\ &= a^2E[X^2] - a^2E[X]^2 \\ &= a^2(E[X^2] - E[X]^2) \\ &= a^2\text{Var}(X) \end{align}\\

Why does E[(X - \mu)^2] equal E(X^2) - \mu^2 ? \begin{align} E[(X - \mu)^2] &= \Sigma_i P()[x_i - \mu]^2\\ &= \Sigma_i P(x_i)[x_i^2 - 2x_i\mu +\mu^2]\\ &= \Sigma_i P(x_i)x_i^2 - 2\mu\Sigma_i P(x_i)x_i + \mu^2 \Sigma_i P(x_i) \end{align} From our definition of E(X) we know that ... \Sigma_i P(x_i)x_i^2 = E(X^2) And... \begin{align} 2\mu\Sigma_i P(x_i)x_i &= 2\mu E(X)\\ &= 2E(X)E(X) \\ &= 2E(X)^2 \end{align} We also know that the sum of all the probabilities in the distribution must sum to 1, so therefore... \mu^2 \Sigma_i P(x_i) = \mu^2 Thus we can say this... \begin{align} E[(X - \mu)^2] &= E(X^2) - 2E(X)^2 + E(X)^2 \\ &= E(X^2) - E(X)^2 \end{align} Yay!

For example, lets say that we have weighted dice so that the probabilities are as follows:

ValueProbability
10.05
20.1
30.1
40.1
50.1
60.55

The population mean, \mu becomes: E[X] = \mu = \sum_x xP(x) = 1\times 0.05 + 0.1 \times 2 + 0.1 \times 3 + 0.1 \times 4 + 0.1 \times 5 + 0.55 \times 6 = 4.75 Of course, the dice does not have a face value of 4.75, but over many many rolls this would be the average score. The variance and standard deviation are calculated in the same way using the above formulas.

Linear Functions Of X

The expected value and variance of a linear function of X is another fairly useful result and we will use it to get some very important results in the section on sampling distributions. For example, we could arbitrarily define a function over dice rolls. Not sure why we'd do this, but say we said the experiement result was g(X) = 2X + 5 where X is the random variable which gives the dice face rolled. Now we have:

g(x)Probability
70.05
90.1
110.1
130.1
150.1
170.55

The expected value of g(x) is therefore: E[g(X)] = \mu = \sum_x xP(x) = 7 \times 0.05 + 0.1 \times 9 + 0.1 \times 11 + 0.1 \times 13 + 0.1 \times 15 + 0.55 \times 17 = 14.5 Interestingly 14.5 = 2 \times 4.75 + 5 ! It looks like E[g(X)] = g(\mu_x) , and for linear functions this is the case (but not so if g(X) is not linear!). When g(X) is LINEAR and g(X) = a + bX : \begin{align} \mu_{g(X)} &= E[a + bX] \\ &= a + b\mu_X \\ \\ \sigma_{g(X)}^2 &= var[a + bX] \\ &= b^2\sigma_X^2 \end{align}

We can derive the first equation as follows, using our first definition of the expected value of a random variable. \begin{align} E[a + bX] &= \sum (a + bx_i)P(x_i) \\ &= \sum aP(x_i) + \sum bx_iP(x_i) \\ &= a + b \sum x_iP(x_i) \\ &= a + bE[X] \\ &= a + b\mu_X \end{align} The same can be done for the variance can also be done in a similar manner. TODO: add this here.

Binomial Distribution

Bernoulli Model

Experiment with two mutually exclusive and exhaustive outcomes. One has the probability p and the other has probability (1-p) . \begin{align} P(0) &= P(fail)\\ &= (1-p) \\ \\ P(1) &= P(success) \\ &= p \end{align} Therefore, using the formulas for mean and variance from the previous sections, we can say the following. \begin{align} \mu_x &= E[X] \\ &= \sum_x xP(x) \\ &= (0)(1-p) + (1)p \\ &= p\\ \\ \sigma_x^2 &= E[(X-\mu)^2] \\ &= \sum(x - \mu_x)^2P(x) \\ &= p(1-p) \end{align}

Binomial Distribution

Bernoulli experiment repeated n times where the repetitions are independent. This is like selection with replacement.

We know from previous discussions that if two events are independent then P(A \cap B) = P(A)P(B) and by extension that P(A \cap B \cap \dots \cap Z) = P(A)P(B) \dots P(Z) . Therefore if I do n experiments and want to know the probablity of m successes in a row and then n-m failures in a row, the probability is: \begin{align} P(m\ successes) &= P(1)P(1)\dots P(1)P(0)P(0)\dots P(0) \\ &= p^m(1-p)^{n-m} \end{align} Where there are m P(1) 's in the above equation and (n-m) P(0) 's. BUT this would be the probability of getting m successes in a row and then (n-m) failures in a row. The question, however, doesn't care about the specific order: we dont care if we get SSFF.. or SFSF... or SSFS... and so on. We need to figure out how many of these combinations there are and account for this!

Let's take a simple example. I have a bag with 5 balls in it: 3 blue, 2 red. What is the probability of drawing 1 blue ball and 1 red ball if I select using replacement (to make the selections independent). Replacement means that what ever ball I pick first, I record the result and then put it back in the bag before making my next pick. In this way, the probability of selecting a particular colour does NOT change per pick.

Note that there are only 2 colours of ball in our bag... this is because we are talking about an experiement where there are only two outcomes, labeled "success" and "failure". We could view selecting a blue as "success" and a red as "failure", or vice versa.

So... selecting a blue and a red ball. Sounds like P(\text{blue}\ \cap\ \text{red}) right? Well, almost, but not quite. Take a look at the sample space below, out of which, the events of interested are highlighted in a light blue colour.

Here I am using an alphabetical subscript to indicate the specific ball. I.e. B_x is a different ball to B_y . The order of selection is given by the order of writing. I.e., " B_x\ B_y " means B_x was picked on the first turn and then B_y was picked on the second turn.

... B_x B_y B_z R_x R_y
B_x B_x B_x B_x B_y B_x B_z B_x R_x B_x R_y
B_y B_y B_x B_y B_y B_y B_z B_y R_x B_y R_y
B_z B_z B_x B_z B_y B_z B_z B_z R_x B_z R_y
R_x R_x B_x R_x B_y R_x B_z R_x R_x R_x R_y
R_y R_y B_x R_y B_y R_y B_z R_y R_x R_y R_y

There are two clear groups of outcomes that will satisfy the question. We see that in one group we drew a red ball first and in the other we drew a blue ball first. So, there are 5 \times 5 total possible events, and of these 6 + 6 are of interest. Therefore, \begin{align} P(\text{drawing a blue and a red}) &= \frac{6}{25} + \frac{6}{25} \\ &= 2 \times \frac{6}{25} \end{align} But, hang on minute! Isn't P(\text{drawing a blue and a red}) the same as P(B \cap R) ?! Well, no, as we can see below... P(B \cap R) = P(B) \times P(R) = \frac{3}{5} \times \frac{2}{5} = \frac{6}{25} So the two expressions are clearly not the same thing. To clear up my confusion I asked the guys at Maths Exchange, and got the following awesome answer from a very nice chap named Joriki. Im quoting it (almost) verbatim because it was just so good!

This confusion can be resolved by careful attention to definitions and notation.

Where you write P(B\cap R) , you call the events B and R "a blue" and "a red" respectively. Implicitly you're referring to two different draws (if you were referring to a single draw, you'd have P(B\cap R)=0 ), but you're not distinguishing the events accordingly, and this leads to confusion.

The events you are interested are B_1 , a blue ball is drawn on the first draw, R_1 , a red ball is drawn on the first draw, B_2 , a blue ball is drawn on the second draw, and R_2 , a red ball is drawn on the second draw. We have P(B_1)=P(B_2)=\frac35 and P(R_1)=P(R_2)=\frac25 .

You want to know P((B_1\cap R_2)\cup(B_2\cap R_1)) . Since the events B_1\cap R_2 and B_2\cap R_1 are mutually exclusive, this is P((B_1\cap R_2)\cup(B_2\cap R_1))=P(B_1\cap R_2)+P(B_2\cap R_1)\;, and since the first and second draws are independent, this is \begin{align} P(B_1\cap R_2)+P(B_2\cap R_1) &= P(B_1)P(R_2)+P(B_2)P(R_1) \\ &= 2\cdot\frac35\cdot\frac25 \\ &= 2\cdot P(B)P(R) \\ &= 2\cdot p^1\cdot (1-p)^1 \end{align}

Note, that in Jorki's example R_1 and R_2 do not refer to different balls: the subscripts refer to different draws. Therefore, R_1 and R_2 could be the same red ball drawn on turn 1 and turn 2 .

So, having understood this, we can see that to get the total probability of m successess (1 blue ball) out of n trials (2 selections), in the case where events are independent, we are concerned with the number of combintations in which the events can occur.

The formula for the binomial distribution is... \begin{align} P(m\ \text{successes in $n$ independent trials}) &= P(m) \\ &={_{n}C_m} \cdot p^m \cdot (1-p)^{(n-m)}\\ &= \frac{n!}{m!(n-m)!} \cdot p^m \cdot (1-p)^{(n-m)} \end{align} For m = 0, 1, \dots, n .

This, incidentally is the same as asking for P((n-m)\ \text{failures in $n$ independent trials}) because \begin{align} {_{n}C_{(n-m)}} &= \frac{n!}{(n-(n-m))!(n-m)!}\\ &= \frac{n!}{m!(n-m)!}\\ &= {_{n}C_m} \end{align}

Let's do this to exhaustion... let's imagine another bag. It doesn't matter how many blue and red balls are in there, just so long as I can select 3 blue balls and 1 red. P(\text{blue}) = p and P(\text{red}) = (1-p) . Once we've made this selection of 3 blues, 1 red, the question is, how many ways were there of getting to this outcome. Now let's check our understanding of using combinations (esp. vs. permutations) to get this...

We can draw a little outcome tree as follows:

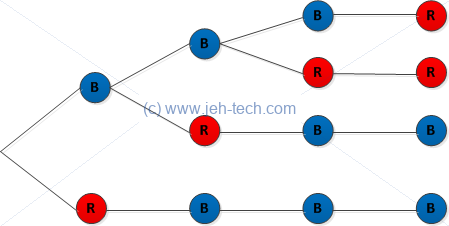
Clearly there are 4 ways to arrive at the selection of 3 blues and 1 red, once we have made that particular selection. Remember we're not asking for a blue/red on a specific turn... we just care about the final outcome, irrespective of the order in which the balls were picked. And we can see... \begin{align} {_4C_3} &= \frac{4!}{3!(4-3)!} &= 4 \end{align}

Why don't we use permutations? The answer is that we don't care if we got B_aB_bB_cR_a or B_bB_aB_cR_a or B_cR_aB_aB_b etc etc, where, as before, the alphabetical substrcipts distinguish the ball, not the turn on which it is drawn as that is given by order of writing.

Having gone through this we can then use the formulas for expected value, or mean, and variance. To make the notation similar to previous examples where we used P(x) , in the above formula I just change m for x so that we get P(x)= \frac{n!}{x!(n-x)!} \cdot p^x \cdot (1-p)^{(n-x)} Where x = 0, 1, \dots, n , meanding that this is the probability of x successes out of n trials.

Recalling that E(X) = \mu = \sum_x xP(x) We can say that the population mean for the Bernoulli distribution is \begin{align} E(X) = \mu &= \sum_{x=0}^{x\le n} x \cdot \left(\frac{n!}{x!(n-x)!} \cdot p^x \cdot (1-p)^{(n-x)}\right) \end{align} And... the rest of the proof gets a little complicated... this PDF by Joel Feldman gives the derivation, which I found by doing a quick google. Liked the explanation.

The population mean and variance are summarised as follows. \begin{align} \mu &= E[X] \\ &= nP\\ \\ \sigma_x^2 &= E[(X - \mu)^2] \\ &= nP(1-P) \end{align}

Often when talking about a binomial distribution you will see something like P(X | n = ?, p = ?) This is the binomial distribution for X successes out of n trials with the probability of success given by p .

We can plot some example distributions... lets do this using Python. 

import matplotlib.pyplot as pl
import numpy as np
from matplotlib.font_manager import FontProperties
from scipy.stats import binom

fontP = FontProperties()
fontP.set_size('small')

n=50
pLst=[0.1, 0.25, 0.5, 0.75, 0.9]
x = np.arange(-1, n+2)
fig, ax = pl.subplots()

for p in pLst:
   dist = binom(n, p)
   ax.plot(x, dist.pmf(x),linestyle='steps-mid')

ax.legend(['$p={}$'.format(p) for p in pLst],
          ncol = 3,
          prop=fontP,
          bbox_to_anchor=[0.5, 1.0],
          loc='upper center')
fig.show()
fig.savefig('binomial_distrib.png', format='png')

Poisson Distribution

Didn't like the starting explanation in [1] so had a look on Wikipedia and found a link to the UMass Amherst Uni's stats page on the Poisson distribution which I though was really well written. That is the main reference here.

Poisson distribution gives the probability of an event occuring some number of times in a specific interval. This could be time, distance, whatever. What matters is that the interval is specific and fixed.

The example used on the UMass Amherst is letters received in a day. The interval here is one day. The poisson distribution will then tell you the probability of getting a certain number of letters in one day, the interval. Other examples could include the number of planes landing at an airport in a day or the number of linux server crashes in a year etc...

The interval is one component. The other is an already observed average rate per interval, or expected number of successes in an interval, \lambda . For example, we might have observed we get on average 5 letters per day ( \lambda=5 ), or that 1003 planes land at our airport ( \lambda=1003 ) per day or that there are 4 linux server crashes per year ( \lambda=4 ) etc...

So, poisson has an interval and an observed average count for that interval. The following assumptions are made:

  • The #occurrences can be counted as an integer
  • The average #occurrences is known
  • The probability of the occurence of an event is constant for all subintervals. E.g., if we divided the day into minutes, the probability of receiving a letter in any minute of the day is the same as for any other minute.
  • There can be no more than one occurrence in the subinterval
  • Occurrences are independent

The distribution is defined as follows, where \lambda is the expected number of events per interval. P(X = x) = \frac{e^{-\lambda}\lambda^x}{x!},\ \ x \ge 0

Eek... didn't like the look of trying to derive the mean and variance. The population mean and variance are as follows. \begin{align} \mu_x &= E(X) = \lambda\\ \\ \sigma^2_x &= E[(X-\mu_x)^2] = \lambda \end{align}

We can plot some example distributions... lets do this using Python. 

import matplotlib.pyplot as pl
import numpy as np
from matplotlib.font_manager import FontProperties
from scipy.stats import poisson

fontP = FontProperties()
fontP.set_size('small')

expectedNumberOfSuccessesLst = [1, 5, 10, 15]
x = np.arange(-1, 31)
fig, ax = pl.subplots()

for numSuccesses in expectedNumberOfSuccessesLst:
   ax.plot(x, poisson.pmf(x, numSuccesses),linestyle='steps-mid')

ax.legend(['$\lambda={}$'.format(n) for n in expectedNumberOfSuccessesLst],
          ncol = 3,
          prop=fontP,
          bbox_to_anchor=[0.5, 1.0],
          loc='upper center')
fig.show()
pl.show()
fig.savefig('poisson_distrib.png', format='png')

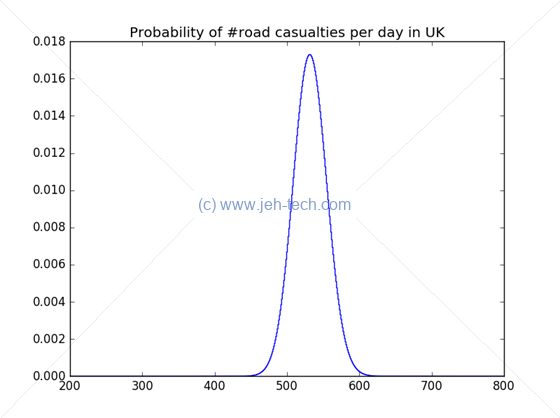
Lets take a little example. Looking at the UK government report on road casualties in 2014, there were a reported 194,477 casualties in 2014. This gives us an average of 532.8137 (4dp) casualties per day! So, we could ask some questions...

What is the probability that no accidents occur on any given day? Recalling that... P(X = x) = \frac{e^{-\lambda}\lambda^x}{x!} We will set \lambda = \frac{194,477}{365} and x = 0 and plug these into the above forumla... \begin{align} P\left(X = 0 | \lambda = \frac{194,477}{365}\right) &= \frac{e^{\left(-194,477/365\right)}{\left(\frac{194,477}{365}\right)}^0}{0!}\\ &= \frac{e^{\left(-194,477/365\right)}\times 1}{1}\\ &= 3.998994e-232 \end{align} Okay... so the probability that on any given day in the UK that there are no road casualties is pretty (very scarily) small!

Of course, we could critisize this analysis as not taking into account seaons, or weather conditions etc etc. In winter, for example, when the roads are icy one might expect the probability of an accident to be greater, but for the purposes of a little example, I've kept it simple.

We might also ask, what is the probability that the number of casualties is less than, say, 300? P(X \lt 300) = \sum_{x=0}^{299} P(X = x) Eek! Don't really want to be calculating this by hand so let's use Python's SciPi package: 

from scipy.stats import poisson
print poisson.cdf(299, 194477.0/365)

This outputs 2.24102710469e-28 which is still pretty unlikely!. For X \lt 400 we get 9.60741455596e-10 , for X \lt 500 we get 0.0783182362497 . So we can imagine that the distribution is really quite steep: 

import matplotlib.pyplot as pl
import numpy as np
from scipy.stats import poisson

x = np.arange(200, 800)
fig, ax = pl.subplots()
ax.plot(x, poisson.pmf(x, 194477/365), linestyle='steps-mid')
ax.set_title('Probability of #road casualties per day in UK')
fig.show()
fig.savefig('poisson_road_fatilities_distrib.png', format='png')

Joint Distributions

When one thing is likely to vary in dependence on another thing. For example, the likely longevity of my milk will correspond to some extent to the temperature of my fridge: there is a relationship between these two variables so it is important that any model produced includes the effect of this relationship. We need to define our probabilities that random variables simultaneously take some values.

Enter the joint probability function. It expresses the probability that each random variable takes on a value as a function of those variables.

A two variable joint probability distribution is defined as: P(x, y) = P(X = x \cap Y = y) This is a subtle difference in the notation of P(x,y) from our previous examples in the starting sections where we wrote things like P(A \cap B) . The former is a distribution where the random variables simultaneously take on the values x and y respectively and the latter is just the probability of two individual events happening simultaneously.

The marginal probabilities are the probabilities that one random variable takes on a value regardless of what the other(s) are doing. In our two variable distribution we have: \begin{align} P(x) &= \sum_y P(x,y) \\ \\ P(y) &= \sum_x P(x,y) \end{align}

Joint probability functions have these properties:

  1. 0 \le P(x,y) \le 1 for any pair of values x and y ,
  2. The sum of the join probabilities is 1.

The conditional probability function looks like this... \begin{align} P(y | x) = \frac{P(x, y)}{P(x)}\\ \\ P(x | y) = \frac{P(x, y)}{P(y)} \end{align}

The random variables are independent if their joint probability function is the product of their marginal probability functions: P(x,y) = P(x)P(y) \implies \text{independence} When they are independent we also have \begin{align} \text{independence} &\implies P(y | x) = P(y)\ \text{and}\\ &\implies P(x | y) = P(x) \end{align}

The conditional mean and variance are: \mu_{Y|X} = E[Y|X] = \sum_Y y P(y|x)\ \text{and}\\ \\ \mu_{X|Y} = E[X|Y] = \sum_X x P(x|y)

Covariance and Correllation

Measure of joint variablility: the nature and strength of a relationship between two variables.

Covariance between two random variables X and Y is Cov(X,Y) , given by: \begin{align} Cov(X,Y) &= E[(X-\mu_x)(Y-\mu_y)] \\ &= \sum_x\sum_y(x - \mu_x)(y-\mu_y)P(x,y) \end{align} This is equivalent to the following: \begin{align} Cov(X,Y) &= E[XY] - \mu_x-\mu_y \\ &= \sum_x\sum_y xyP(x,y) - \mu_x\mu_y \end{align} A covariance that is strongly negative indicates a good inverse linear relationship. Strongly positive indicates a good linear relationship and near zero indicates no relationship. Note that if two random variables are statistically independent, the covariance between them is (near) zero. But, if the covariance is (near) zero it does not necessarily mean there is no relationship, it might just not be linear.

Correlation is just a "normalisation" of the covariance such that the measure is limited to being in the range [-1, 1]. Corr(X,Y) = \frac{Cov(X,Y)}{\sigma_x\sigma_y}

This YouTube video explains the difference really well:

Continuous Distributions

Cumulative Distribution Function (CDF)

CDF gives probability that continuous random variable X does not exceed a particular value, x : CDF(x) = P(X \lt x) The probability that X takes on a signular value is zero. I.e., P(X == x) = 0 . Therefore, it doesn't matter if we write \lt or \le ...

To get the probability that X lies within a range use: \begin{align} P(x_1 \lt X \lt x_2) &= CDF(x_2) - CDF(x_1)\\ &= P(X \lt x_2) - P(X \lt x_1) \end{align}

Probability Density Function (PDF)

Call our PDF f(x) ... Then the total area under the curve f(x) is 1. I.e., \int_{-\infty}^{\infty} f(x) \mathrm dx = 1.0 The probability that X takes a value between two limits is... P(x_1 \lt X \lt x_2) = \int_{x_1}^{x_2} f(x) \mathrm dx And the CDF is also defined by.... CDF(x_0) = \int_{min(X)}^{x_0} f(x) \mathrm dx We can judge whether a distribution is a valid PDF using the above definitions.

Uniform Distribution

The uniform distribution is one where the probability that X takes a value in a fixed size interval is the same regardless of where the interval "starts" (as long as the interval is contained entirely within the range for which X is non-zero). I.e, f(x) = \begin{cases} \frac{1}{x_u - x_l}, &x_l \le X \le x_u\\[2ex] 0, &\text{otherwise} \end{cases}

Normal Distribution

This distribution is defined by a gaussian bell-shaped curve. The probability distribution function for a normally distributed random vairable, X , is given by this equation: f(X = x) = \frac{1}{\sqrt{2\pi\sigma^2}} \cdot e^{-{(x-\mu)^2}/{2\sigma^2}} For any normal distribution the following applies:

  1. About 68% of the data will fall within one standard deviation, \sigma , of the mean, \mu ,
  2. About 95% of the data will fall within two standard deviations, 2\sigma , of the mean, \mu ,
  3. Over 99% of the data will fall within three standard deviations, 3\sigma , of the mean, \mu ,
  4. Mean is E[X] = \mu ,
  5. Variance is Var(X) = E[(X - \mu)^2] = \sigma^2 ,

The normal distribution is defined with the following notation: X \sim N(\mu, \sigma^2) There is no simple algebraic expression for the cummulative distribution function. Can't really say I fancy the idea of integrating the above function! There are many numerical approximations. Computer could do it for us, but another way is to convert every normal distribution to the standard normal distribution.

The standard normal distribution is a normal distribution where the the mean is 0 and the variance is 1: Z \sim N(0, 1) And Z = \frac{X - \mu}{\sigma} In English we can say that the z-score/value is the number of standard deviations X is away from the (population) mean \mu .

To solve P(a \lt X \lt b) we solve the following: P\left( \frac{a - \mu}{\sigma} \lt Z \lt \frac{b - \mu}{\sigma}\right) For which we can consult a standard normal table.

We can also get the probability of a Z score and vice versa in Python by using scipy.stats.norm.cdf() and scipy.stats.norm.ppf() respectively as documented here.

Percentiles

Wikipedia defines a percentile as a measure giving the value below which a given percentage of obersvations fall. If an observation is AT the xth percentile then it has the value, V, at which x% of the scores can be found. If it is IN this percentile then its value is in the range 0 to V.

Percentiles aren't really specific to normal distributions but you often get asked questions like "what is the 95th percentile of this distribution?"

In the standard normal distribution...

  1. 90th percentile is at z=1.28. (This is because P(z < 1.28) = 90% ).
  2. 95th percentile is at z=1.645. (This is because P(z < 1.645) = 95% ).
  3. And so on...

Sampling Distributions

A Little Intro...

So far we have been talking about population statistics. The values \mu and \sigma have been the mean and standard deviation of the population. However, generally it is pretty impossible to gather information about an entire population: this can be due to the cost that would be involved, or perhaps that time that such an endevour would take, for example. It might also be undesirable to analyse an entire population if, for example, analysis involved destruction of the samples taken!

So, what is normally done is to take a sample from the population and then use the sample statistics to make inferences about the population statistics. The image below shows three samples that have been taken from a population. Each sample set can, and will most probably, have a different shape, mean, and variance!

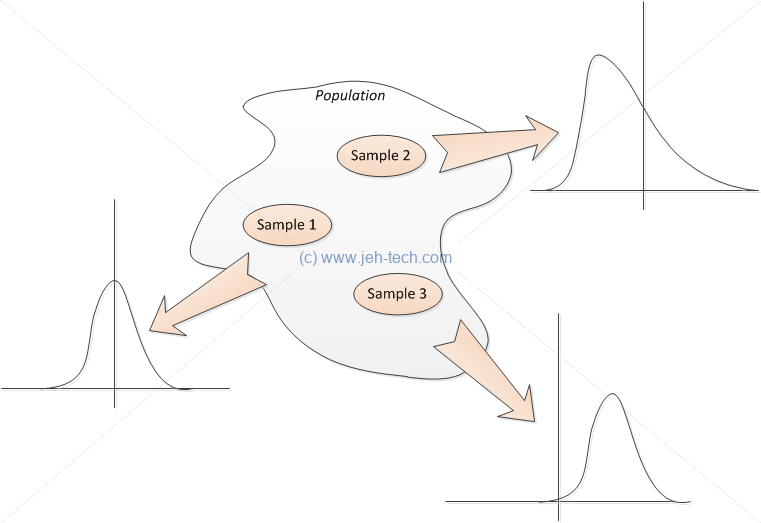
Picture of taking different samples from a population and the sample distributions

We can demonstrate this concept using a quick little Python program to take 4 samples from the normal distribution where each sample has 10 members: 

import numpy as np
import matplotlib.pyplot as pl

numSampleSets = 4
numSamplesPerSet = 10

# Limit individual plots, otherwise the first plot takes forever and is rubbish
doShowIndividualSamples = (numSampleSets <= 8) and (numSamplesPerSet <= 50)

# Create a numSampleSets (rows) x numSamplesPerSet (cols) array where we use
# each row as a sample.
randomSamples = np.random.randn(numSampleSets, numSamplesPerSet)

# Take the mean of the rows, i.e. the mean of each sample set
means = randomSamples.mean(axis=1)

if doShowIndividualSamples:
   fig, axs = pl.subplots(nrows=int(numSampleSets/2.0+0.5), ncols=2)
   xticks = np.arange(numSamplesPerSet, dtype='float64')
   for idx in range(numSampleSets):
         ax_col = idx % 2
         ax_row = int(idx/2.0)
         thisAx = axs[ax_row][ax_col]
         thisAx.bar(xticks, randomSamples[idx][:], width=1)
         thisAx.set_xticks(xticks + 0.5)
         thisAx.set_xticklabels(xticks, fontsize=8)
         thisAx.axhline(y=means[idx], color="red", linewidth=2)
         thisAx.set_title("Sample set #{}".format(idx))
         thisAx.grid()

xticks = np.arange(numSampleSets, dtype='float64')
fig2, ax2 = pl.subplots(nrows=2)
ax2[0].bar(xticks, means)
ax2[0].grid()
ax2[0].set_title("Distribution of {} sample means (n={})".format(numSampleSets, numSamplesPerSet))
ax2[0].set_ylabel("Mean value")
ax2[0].set_xlabel("Sample set #")

ax2[1].hist(means, 50)
ax2[1].grid()
ax2[1].set_title("Histogram of {} sample means (n={})".format(numSampleSets, numSamplesPerSet))
ax2[1].set_ylabel("# sample mean's")
ax2[1].set_xlabel("Sample mean bin")

pl.tight_layout()
pl.show()

The script above produces the following graphs. The x-axis is just the sequence number of the sample member and the y-axis the value of the sample member. The horizontal line is the sample mean.

Graphs of separate samples from normal distribution showing how sample mean varies between samples

We can see from this little example that the samples in each of the 4 instances are different and that the mean is different for each sample. Keep in mind that the graph shown when you run the above script will be different as it is a random sample :)

So we can see that although the population mean is fixed the sample mean can vary from sample to sample. Therefore, the mean of a sample is itself a random variable and as a random variable it will have it's own distribution (same applies for variance).

But, we want to use the sample statistics to infer the population statistics. How can we do this if the sample mean (and variance) can vary from sample to sample? There are a few key statistical theories that will help us out...

Independent and Identically Distributed (I.I.D.) Random Variables

Wikipedia says that ...a sequence or other collection of random variables is independent and identically distributed (I.I.D.) if each random variable has the same probability distribution as the others and all are mutually independent...

It is often the case that if the population is large enough and a sample from the population only represents a "small" fraction of the population that a set of simple random samples without replacement still qualifies I.I.D. selections. If you sample from a population and the sample size represents a significant fraction of the population then you cannot assume this to be true.

We're going to need to know this a little later on when we talk about conistentent estimators and the law of large numbers...

The Law of Large Numbers

The law of large numbers states that the average of a very large number (note we haven't quite defined what "very large" is) of items will tend towards the average of the popultion from which the items are drawn. I.e., the sample mean (or any other parameter) tends towards the population mean (or parameter, in general) as the number of items in the sample tends to infinity.

This is shown empirically in the example below: 

import numpy as np
import matplotlib.pyplot as pl

maxSampleSizes = [100, 1000, 100000]
fig, axs = pl.subplots(nrows = 3)
for idx, ssize in enumerate(maxSampleSizes):
   sample_sizes = np.arange(1,ssize+1)
   sample_means = np.random.randn(ssize).cumsum() / sample_sizes
   axs[idx].plot(sample_sizes, sample_means)
   axs[idx].set_xlabel("Sample size, max is {}".format(ssize));
   axs[idx].set_ylabel("Average")
   axs[idx].axhline(y=0, color="red")

fig.show(); pl.show()

Explain the code a little... np.random.randn(ssize) generates a numpy array with ssize elements. Each element is a "draw" from the standard normal distribution. The function cumsum() then produces an array of ssize elements where the second element is the sum of the first 2 elements, the third element is the sum of the first 3 elements and so on. Thus we have an array where the ith element is the sum of i samples. Dividing this by the array sample_sizes gives us an array of means where the ith element is the mean of a sample with i items.

Running the code produced the figure below...

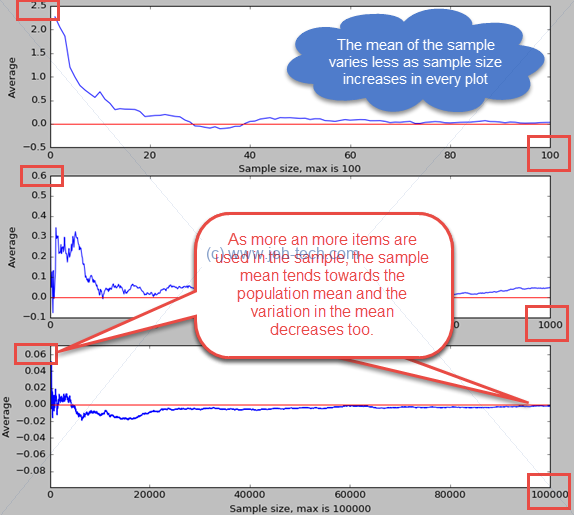
To summarise, the law of large numbers states that the sample mean of I.I.D. samples is consistent with the population mean. The same is true for sample variance. I.e., as the number of items in the sample increases indefinitely, the sample mean will become a better and better estimate of the population mean.

Sampling Distribution Of The Sample Mean

We've established that between samples, the mean and variance of the samples, well... varies! This implies that we can make a distribution of sample means.

The "sampling distribution of the sample mean" (a bit of a mouthful!) is the probability distribution of the sample means obtained from all possible samples of the same number of observations.

That's a bit of a mounthful! What it means is that if we took, from the population, the exhaustive set of all distinct samples of size n , and then took the mean of each sample, we could figure out what the propability is that any sample of size n has a specific mean. Thus we build up the probability distribution of sample means, where the sample size is n . We will see that this probability distribution is centered around the mean of all the sample means and that it also has a normal distribution (see LLN and CLT).

For example if I am a factory owner and I produce machines that accurately measure distance, I could have a population of millions. I clearly do not want to test each and every device coming off my production line, especially if the time that testing requires is anything approaching the time taken to produce the item: I'd be halving (or more) my production throughput!

So what do I do? I can take a sample of say 50 devices each day. I can test these to see if they accurately measure distance, and if they do I can assume the production process is still running correctly.

But as we have seem if I test 50 devices each day for 10 days, each of my 10 sample sets will have a different mean accuracy. On the first day, the mean accuracy of 50 devices might be 95%, on the second day, the mean of the next 50 devices might be 96.53% and so on.

The sample mean has a distribution. As we can take many samples from a population we have sampled the sample mean, so to speak, hence the rather verbose title "sampling distribution of the sample mean".

Now, I can ask, on any given day, "what is the probability that the mean accuracy of my 50 devices is, say 95%?". This is the sampling distribution of the sample mean: the probability distribution of the sample means (mean accuracy of a sample of devices) obtained from all possible samples (theoretical: we can't actually measure all possible samples!) of the same number of observations (50 in this case).

The law of large numbers gives us a little clue as to how variable the sample means will be... we know that if the sample size is large then the sample mean tends towards the population mean as has a much narrower variance about the population mean. So, 50 samples is better than 10. But 10,000 samples would be even better. The question is how many samples do we need. Will try to answer that (much) later on...

Sample Mean And It's Expected Value (The Mean Of Sample Means)

Continuing with the example of distance measurement devices. We could say each device in our sample set is represented by random variables A_1, A_2, ..., A_{50} (we samples 50 devices each day). We can generalise this to m devices in the sample set. Using our definition of expected value we can define the sample mean as the random variable \overline A_i , for the ith sample set of, and is defined as follows. \overline X_i = \frac{1}{m}\sum_{i=1}^m A_i

Now we can calculate the expected value of the sample mean, E(\overline X) (the mean of the sample means).

Imagine that we take n samples, where each sample is a set of m devices from our population. If we represent the mean of each sample as the random variables \overline X_1, \overline X_2, \cdots, \overline X_n , then the expected value of the distribution of sample means is the mean expected value of the samples... E(\overline X) = E\left(\frac{1}{n}(\overline X_1 + \overline X_2 + \cdots + \overline X_n)\right) We saw that expected value of a linear combination of random variables is the linear combination of each random variable's expected value. This means that we can write the following. E(\overline X) = \frac{1}{n}\left[E(\overline X_1) + E(\overline X_2) + \cdots + E(\overline X_n)\right] The law of large numbers also tells us that if the size of each sample is sufficiently large, it's sample mean, \overline{X_i} will tend towards the population mean, \mu . So, if m is large enough we can say... \begin{align} E(\overline X) &= \frac{1}{n}\left[\mu + \mu + \cdots + \mu\right]\\ &= \frac{n\mu}{n}\\ &= \mu \end{align} for the This means that the mean of "the sample distribution of sample means" is the population mean when the size of each sample ( m ) is sufficiently large. Put another way, the distribution of samples means in centred around the population mean.

A single sample mean can therefore be larger or smaller than the population mean, but on average, there isn't any reason to expect that it is either. As the sample size increases we also know that the likelihood of the sample mean being higher or lower than the population mean decreases (law of large numbers).

The Variance Of The Sample Mean w.r.t. Sample Size And Standard Error

Sample variance can be written as \sigma_{\overline X}^2 or S^2 . \text{Var}(\overline X) = \sigma_{\overline X}^2 = S^2 = \frac{\sigma^2}{n} We can see that variance of the sampling distribution decreases as sample size increases. Therefore the larger the sample the more accurately we can infer population statistics.

How did we get the above results? Well, it all is a bit brain melting, but here goes. The variance of the mean of sample means is written as \text{Var}(\overline X) . Because it is the variance of the mean of sample means, we can write this: \text{Var}(\overline X) = \text{Var}\left(\frac{1}{n} \sum_{i=1}^{i \le n} \overline X_i\right) The constant n can be taken out of the variance. TODO - finish this off.

The sample standard deviation is often refered to as the standard error. \text{Standard error} = \sigma_{\overline X} = \frac{\sigma}{\sqrt n} If sample size not super small compared to population use finite population correction factor \frac{N-n}{N-1} to get \text{Var}(\overline X) = \frac{\sigma^2}{n} \cdot \frac{N-n}{N-1}

The Shape Of The Samplign Distribution Of Sample Means

When samples are selected from a population that has a normal distribution we will see (anecdotally) that the sampling distribution of sample means is also normally distributed.

A histogram of the sample means gives a better picture of the distribution of sample means from the 4 sample sets. Diagrams have been drawn using the previous python example.

Graphs of separate samples from normal distribution showing how sample mean varies between samples

Now observe what happens when we increase the number of sample sets taken to 50. The distribution of sample means is still pretty distributed without much definition of the shape of the distribution...

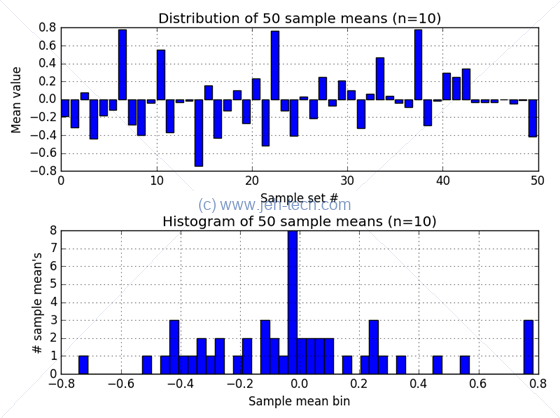
Graphs of separate samples from normal distribution showing how sample mean varies between samples

Now observe what happens when we increase the number of sample sets taken to 1000. The distribution of sample means begins to take shape...

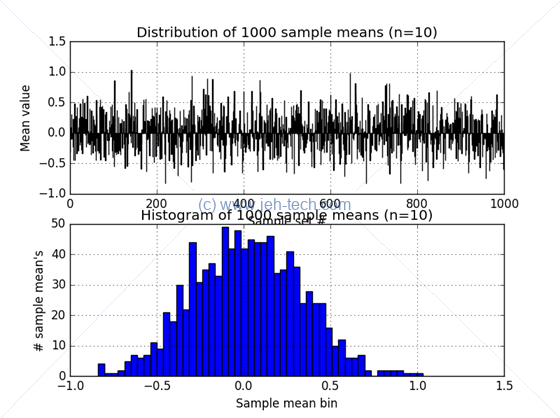
Graphs of separate samples from normal distribution showing how sample mean varies between samples

Now observe what happens when we increase the number of sample sets taken to 1000. The distribution of sample means now really looks very much like a gaussian distribution... interesting!

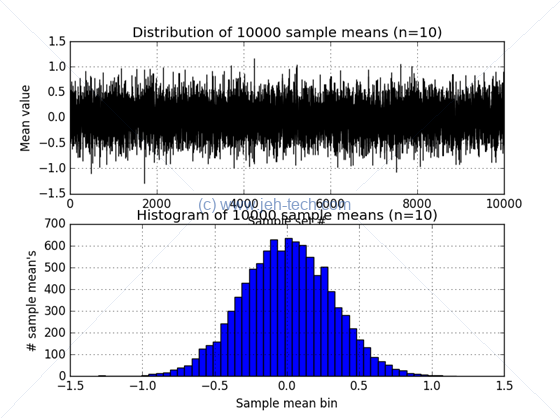
Graphs of separate samples from normal distribution showing how sample mean varies between samples

Clearly when we sample from the population the sample can be, to varying degrees, either a good or bad representation of the population. To help ensure that that sample represents the population (i.e., no "section" of the population is over or under represented) a simple random sample is usually taken.

Also of great interest in the above is that as the number of samples taken increases the distribution of sample means appears to become more and more gaussian in shape!. What is always true, and even more important is that the sampling distribution becomes concentrated closer to the population mean as the sample size increases, as we have seen in the maths earlier. The example above also doesn't proove it... its just anecdotal evidence. We could also notice that as #samples increases the variance of the sample mean decreases, again as we saw in the maths earlier.

Remember: take care to differentiate between the sample mean, \overline x , sometimes witten as \mu_{\overline X} , and the population mean, \mu . We do not know the population mean. We know the sample mean. The population mean is fixed. The sample mean, as seen, will vary between samples.

We must also remember to differentiate between the sample variance, \sigma_{\overline X}^2 and the population variance, \sigma^2 . We do not know the population variance. We know the sample mean. The population variance is fixed. The sample variance, as seen, will vary between samples.

Also remember that the samples were drawn from a population that is normally distributed. So the sampling distribution was also normally distributed, as we have anacdotally seen. The central limit theory (CLT) will show us that is doesn't matter what the population distriution is. Enough samples and the sampling distribution of the sample mean will always tend towards normal distribution.

Because the sampling distribution of sample means is normally distributed, it means that we can also form a standard normal distribution for the sample means, which we do as follows: \begin{align} Z &= \frac{\overline X - \mu}{\sigma_{\overline X}} \\ &= \frac{\overline X - \mu}{\frac{\sigma}{\sqrt n}} \end{align}

Central Limit

We saw that the mean of the sampling distribution of sample means is E(\overline X) = \mu and that the variance of the sample mean is \text{Var}(\overline X) = \frac{\sigma^2}{n} . We also know (although I haven't shown this... I haven't bothered looking up the proof either!) that the sampling distribution of sample means is also normal.

The central limit theorem removes the restriction that the population we draw from need be normally distributed in order for the sampling distribution of the sample mean to be normally distributed. The central limit theoem states that the mean of a random sample drawn from a population with any distribution will be approx. normally distributed as the number of samples, n , becomes large.

We could test this for, say, samples drawn from the binomial distribution. We have to modify our python code a little though (and also slim line some of the bits out)... 

import numpy as np
import matplotlib.pyplot as pl

numSampleSets = 4000
numSamplesPerSet = 10
p = 0.5

# Make an array of numSampleSets means of samples of size numSamplesPerSet
# drawn from the binomial distirbution with prob of success `p`
means = np.random.binomial(numSamplesPerSet, p, numSampleSets)
means = means.astype("float64") / numSamplesPerSet

xticks = np.arange(numSampleSets, dtype='float64')
fig2, ax2 = pl.subplots()
ax2.hist(means, 50)
ax2.grid()
ax2.set_title("Histogram of {} sample means (n={})\nSamples draw from binomian p={}".format(numSampleSets, numSamplesPerSet, p))
ax2.set_ylabel("# sample mean's")
ax2.set_xlabel("Sample mean bin")

pl.tight_layout()
pl.show()

When we set the number of sample sets taken to be small, at 10, we get this:

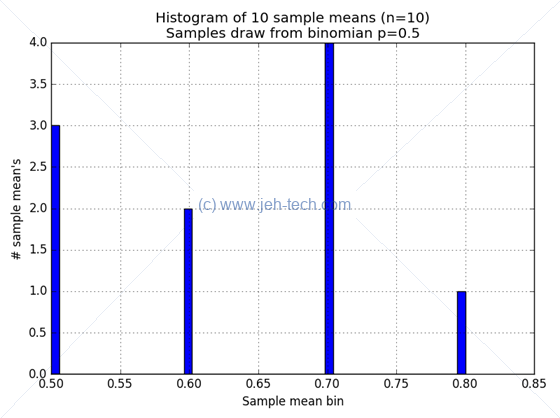
When we set the number of sample sets taken to be very large, at 4000, we get this:

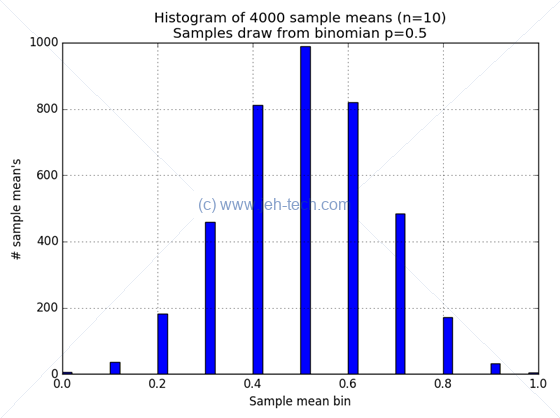
Hmmm... anacdotally satisfying at least.

Confidence Intervals

The following is mostly based on this Khan Achademy tutorial with some additions from my reference textbook.

A confidence interval is a range of values which we are X% certain contain an unknown population parameter (e.g. the population mean), based on information we obtain from a sample. In other words, we can infer from our sample something about an unknown population parameter.

Let's go back to our distance measurement devices. I have a test fixture that is exactly 100cm wide. Therefore a device should, when placed in this fixture, report/measure a distance of 100cm +/- some tolerance.

Remember that I don't want to test all of the sensors I've produced because this will kill the manufacturing time and significantly raise the cost per unit. So I've decide to test, let's say, 50 sensors.

As I test each device in my sample of 50 I will get back a set of test readings, one for each device. 100.1cm, 99cm, 99.24cm, ... etc. From the sample I can calculate sample mean and sample variance. But this is about all I know: I do not know my population mean or population variance!

But I have learn't something about the sampling distribution of sample means. To recap, we have seen that: E(\overline X) = \mu The expected value of the sample mean (i.e., the mean of all possible sample means) is the same as the population mean for large enough samples. \text{Var}(\overline X) = \frac{\sigma^2}{n} The variance of the sample mean is related to the poulation variance by sample size.

So, I also know that my specific sample mean must lie somewhere in the sampling distribution of sample means...

Continuing with the example then... let's say I have taken my sample of 50 devices. I have a sample mean of \overline x = 105\text{cm} . This is shown in the graph of the sampling distribution of sampling means below. In this distribution my specific sample has a mean that lies somewhere in this distribution.


<Click me to toggle code view for graph creation> 

import matplotlib.pyplot as pl
import numpy as np
import scipy.stats

sample_mean = 105
population_mean = 99
expected_sample_mean = 102
var_of_expected_sample_mean = 4
std_of_expected_sample_mean = np.sqrt(var_of_expected_sample_mean)

x = np.linspace( expected_sample_mean - 4 * var_of_expected_sample_mean
               , expected_sample_mean + 4 * var_of_expected_sample_mean
               , 500)
y = scipy.stats.norm.pdf( x
                        , loc   = expected_sample_mean
                        , scale = var_of_expected_sample_mean)

max_y = scipy.stats.norm.pdf( expected_sample_mean
                            , loc   = expected_sample_mean
                            , scale = var_of_expected_sample_mean)

fig, ax = pl.subplots()
ax.plot(x,y)
fill_mask = (x >= expected_sample_mean) & (x <= expected_sample_mean + std_of_expected_sample_mean)
ax.fill_between(x, 0, y
               , where       = fill_mask
               , interpolate = True
               , facecolor   = 'lightblue')

ax.annotate(r'$E(\overline{X}) = \mu$',
            xy=(expected_sample_mean, 0),
            xytext=(expected_sample_mean-2*var_of_expected_sample_mean, 0.02),
            bbox=dict(fc="w"),
            fontsize='large',
            arrowprops=dict(facecolor='black', shrink=0.05, connectionstyle="arc3,rad=0.2", fc="w"))


ax.annotate(''
      , xy=(expected_sample_mean, max_y/2)
      , xytext = (expected_sample_mean + std_of_expected_sample_mean, max_y/2)
      , arrowprops=dict(arrowstyle="<->"
                       , connectionstyle="arc3"
                       )
      )

ax.annotate(r'$\sigma_{\overline{X}} = \frac{\sigma}{\sqrt{n}}$',
            xy=(expected_sample_mean + std_of_expected_sample_mean/2, max_y/2),
            xytext=(expected_sample_mean + 2*std_of_expected_sample_mean, 3*max_y/4),
            fontsize='large',
            bbox=dict(fc="w"),
            arrowprops=dict(facecolor='black', shrink=0.05, connectionstyle="arc3,rad=0.2", fc="w"))


ax.axvline(x=population_mean, color='black', lw=2)
ax.annotate('Population mean, $\\mu$,\nis unknown!',
            xy=(population_mean, max_y/2),
            xytext=(x[0], 3*max_y/4),
            bbox=dict(fc="w"),
            arrowprops=dict(facecolor='black', shrink=0.05, connectionstyle="arc3,rad=0.2", fc="w"))

ax.axvline(x=sample_mean, color='black', lw=2)
ax.annotate('Sample mean, $\\overline{{x}}$,\nis {}'.format(sample_mean),
            xy=(sample_mean, max_y/2),
            xytext=(sample_mean + 2*std_of_expected_sample_mean, max_y/4),
            bbox=dict(fc="w"),
            arrowprops=dict(facecolor='black', shrink=0.05, connectionstyle="arc3,rad=0.2", fc="w"))

ax.set_title("An example sampling distribution of sample means\nfor the distance measurement devices")
ax.grid()
pl.show()

The graph above also shows the population mean. This also lies somewhere in this distribution of sample means, but we don't know where. This is the parameter that we want to infer! The single sample's mean and variance are all we have at the moment so somehow we need to move from these statistics to an assertion about the population mean.

Now I'm going to stop talking about \overline x , our specific sample mean. This is because we are taking about any sample, so we want to use a random variable that represents the mean of a random sample, \overline X .

We know \overline X is somwhere near E(\overline X) and will lie in an interval that spans the distance E(\overline X) \pm \text{interval} . But how big is this interval? To be certain that it contains our sample mean it would have to be infinitely wide! So we can't be certain. But, we could be pretty certain. We could, for example, say we'd be satisfied if we were 95% certain that \overline X \in E(\overline X) \pm \text{interval} ... In other words we are asking the following question, what is... P(E(\overline X) - \text{interval/2} \lt \overline X \lt E(\overline X) + \text{interval/2}) = 0.95\ ?? This interval that gives us a 95% probability that the mean of a random sample (of size 50 in this case) will lie within \text{interval} of the expected sample mean. (It doesn't have to be 95%, you choose how confident you want to be!).

Hang on! We know from the CLT that the sampling distribution should be normal. So we can figure this out using the normal distribution. Further more we know that we can normalise the distribution to arrive at the standard normal distribution. Therefore, what we are looking for in the standard normal is the following:


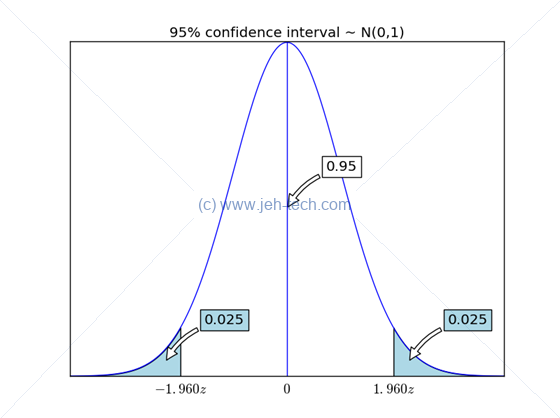
<Click me to toggle code view for graph creation> 

import matplotlib.pyplot as pl
import numpy as np
import scipy.stats


z = np.linspace(-4, 4, 500)
y = scipy.stats.norm.pdf(z)
x_95p = scipy.stats.norm.ppf(0.975) #.025 in each tail gives 0.05 for 95% conf
x95_mid = scipy.stats.norm.ppf(0.9875)

fig, ax = pl.subplots()
ax.plot(z,y)
ax.fill_between(z, 0, y
               , where       = z < -x_95p
               , interpolate = True
               , facecolor   = 'lightblue')
ax.text(-x_95p, -0.02, "$-{0:.3f}z$".format(x_95p), ha="center", fontsize='large')

ax.fill_between(z, 0, y
               , where       = z > x_95p
               , interpolate = True
               , facecolor   = 'lightblue')
ax.text(x_95p, -0.02, "${0:.3f}z$".format(x_95p), ha="center", fontsize='large')

ax.plot( [0, 0], [0, max(y)], color='b')
ax.text(0, -0.02, "$0$", ha="center", fontsize='large')

ax.annotate( "0.025"
           , xy=(x95_mid, scipy.stats.norm.pdf(x95_mid)/2)
           , xytext=(40, 40)
           , textcoords='offset points'
           , bbox=dict(fc="lightblue")
           , fontsize='large'
           , arrowprops=dict(facecolor='black', shrink=0.05, connectionstyle="arc3,rad=0.2", fc="w"))

ax.annotate( "0.025"
           , xy=(-x95_mid, scipy.stats.norm.pdf(-x95_mid)/2)
           , xytext=(40, 40)
           , textcoords='offset points'
           , bbox=dict(fc="lightblue")
           , fontsize='large'
           , arrowprops=dict(facecolor='black', shrink=0.05, connectionstyle="arc3,rad=0.2", fc="w"))

ax.annotate( "0.95"
           , xy=(0, max(y)/2.0)
           , xytext=(40, 40)
           , textcoords='offset points'
           , bbox=dict(fc="w")
           , fontsize='large'
           , arrowprops=dict(facecolor='black', shrink=0.05, connectionstyle="arc3,rad=0.2", fc="w"))

ax.set_xticks([])
ax.set_yticks([])
ax.set_title("95% confidence interval ~ N(0,1)")
pl.show()

And we previously saw how to do this: Z = \frac{\overline X - \mu}{\frac{\sigma}{\sqrt n}} Apply this to the interval P(E(\overline X) - \text{interval/2} \lt \overline X \lt E(\overline X) + \text{interval/2}) = 0.95 Will give us \begin{align} 0.95 &= P(-\text{normalised interval/2} \lt Z \lt \text{normalised interval/2}) \\ &= P(-\text{normalised interval/2} \lt \frac{\overline X - \mu}{\frac{\sigma}{\sqrt n}} \lt \text{normalised interval/2}) \end{align} And we know how to calculate this "normalised interval" It is the Z value that will give us the 95% condifence interval we see above, and this Z value is, by consulting tables, 1.96. \begin{align} 0.95 &= P(-1.96 \lt \frac{\overline X - \mu}{\frac{\sigma}{\sqrt n}} \lt 1.96) \end{align} Re-arange this a little... \begin{align} 0.95 &= P(-1.96 \lt \frac{\overline X - \mu}{\frac{\sigma}{\sqrt n}} \lt 1.96) \\ &= P(-1.96\cdot \frac{\sigma}{\sqrt n} \lt \overline X - \mu \lt 1.96\cdot \frac{\sigma}{\sqrt n}) \\ &= P(-1.96\cdot \frac{\sigma}{\sqrt n} - \overline X \lt - \mu \lt 1.96\cdot \frac{\sigma}{\sqrt n} - \overline X) \\ &= P(\overline X + 1.96\cdot \frac{\sigma}{\sqrt n} \gt \mu \gt \overline X - 1.96\cdot \frac{\sigma}{\sqrt n} ) \text{ (multiply by -1 reverses inequalities)}\\ &= P(\overline X - 1.96\cdot \frac{\sigma}{\sqrt n} \lt \mu \lt \overline X + 1.96\cdot \frac{\sigma}{\sqrt n} ) \\ \end{align} And... oh! I know my sample mean. Lets say it was 99.5cm... then I have \begin{align} 0.95 &= P(99.5 - 1.96\cdot \frac{\sigma}{\sqrt n} \lt \mu \lt 99.5 + 1.96\cdot \frac{\sigma}{\sqrt n} ) \end{align} Ah crap, I don't know the population standard deviation. But I do know my sample standard deviation. If my sample size is large enough the LLN says it will be a consistent estimator of the population standard deviation. So we'll approximate and say... \begin{align} 0.95 &= P(99.5 - 1.96\cdot \frac{s}{\sqrt n} \lt \mu \lt 99.5 + 1.96\cdot \frac{s}{\sqrt n} ) \end{align} Okay, lets say my sample had a standard deviation of 0.5cm. Then we get... \begin{align} 0.95 &= P(99.5 - 1.96\cdot \frac{0.5}{\sqrt{50}} \lt \mu \lt 99.5 + 1.96\cdot \frac{0.5}{\sqrt{50}} ) \end{align} Well this is great, we now know that the population mean is somewhere in the interval 99.5 \pm 1.96\cdot \frac{0.5}{\sqrt{50}} with a 95% confidence! I.e. we are 95% confident that the population mean lies somewhere between 99.35cm and 99.64cm. So we can conclude that our production process is producing instruments that slightly underestimate distance.

Quite a few assumptions and estimates have been made here. I assumed that I could estimate the population standard deviation with my sample's standard deviation. This could be okay for large sample sizes from an even larger population, but when this is not the case, this assumption breaks down. Something called the "Student-t" distribution will cope with this and we'll come to that later.

Kalman Filter

ttp://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/